Time Limit: 3s → 5s
题目背景
安宁顷刻今将逝,末日黑云伺隙来。宿命无情何所惧?越其止境冀花开。
为了执行毁灭世界的疯狂计划,一位占用了已死之人躯壳的神秘男子在这颗蓝色的星球上创造出了无数末日塔。这些末日塔会散发出浓密的以太射线,对末日塔附近的几乎所有生物进行精神控制,只有受到特殊加护的人才能免受以太射线控制。
一些受到加护的义勇队对这些末日塔进行了调查,其结果显示:这些末日塔组成了复杂的以太传输网络,持续不断地从大地中吸收以太,并将以太传输到位于帝国的中枢塔。
一队持有特殊加护的英雄决定闯入其中一些末日塔,以期彻底调查并尝试破坏这些末日塔。英雄们破坏掉进入的末日塔后,以太传输网络就会受到影响,因此大家希望选择一些末日塔,将其破坏后能使得网络的最大传输容量降到最低。
作为勇闯末日塔小队的先锋,你再次阅读了小队目前所掌握的所有信息。这次大胆的行动计划最终能否拯救这个世界,眼下恐怕谁都无法事先料定。但为了这颗星球的未来,我们只能放手一搏。
题目描述
星球的表面是一个中心位于 $(0, 0, 0)$,半径为 $R$ 的完美球面。星球表面上共有 $N$ 座末日塔,这些令人毛骨悚然的塔构成了以太传输网络的所有节点。
- 末日塔的高度远小于星球半径,因此我们认为第 $i (1 \le i \le N)$ 座塔是球面上的一个点 $\left(x_i, y_i, z_i\right)$。第 $i$ 座塔的以太传输效率为 $q_i$。
- 保证 $N$ 座末日塔的位置两两不同。在这 $N$ 座末日塔中,$s$ 号塔是以太吸收点,$t$ 号塔是位于帝国的中枢塔;这两座塔的以太浓度显著高于其它的末日塔,因此只能闯入这两座塔之外的末日塔。
$N$ 座末日塔之间共有 $M$ 条传输通道。第 $j (1 \le j \le M)$ 条传输通道连接 $u_j, v_j$ 两座末日塔,让它们可以互相传输以太。
- 传输通道是双向的,但单位时间内以太的流向必须是单向的。
- 为了节省不必要的成本,传输通道的两端不会连接相同的塔,也不会有两条传输通道连接相同的末日塔对。
- 为了降低传输距离,第 $i$ 条传输通道沿着 $u_j$ 和 $v_j$ 所在的大圆的劣弧铺设,故其长度 $r_j$ 为两座末日塔在星球表面的球面距离。为了避免传输通道的互相干扰,对于任意一条传输通道所对应的劣弧,其他传输通道所对应的劣弧只会在该劣弧的两端点上与该劣弧相交。保证由同一条传输通道相连的两座末日塔的位置不是对跖点关系。
- 如果不知道大圆、劣弧、球面距离和对跖点是什么,可以参考题面最后的提示部分。
受到传输效率和通道长度的影响,每条传输通道有各自传输以太的容量上限。
- 具体而言,每个单位时间内,第 $j$ 条传输通道的容量上限为 $\frac{Kq_{u_j} q_{v_j}}{r_j^2}$,其中 $K$ 是给定的常数,$q_{u_j}, q_{v_j}$ 为该传输通道两端的塔的传输效率,$r_j$ 为这条传输通道的长度。
整张以太传输网络需要将 $s$ 号塔吸收的以太沿着传输通道传输到 $t$ 号塔,并使得单位时间内的以太传输量最大。为此,传输网络会自动确定一个以太传输方案,在满足所有传输通道容量上限的前提下,最大化这一传输量。
- 换句话说,如果将末日塔看作图上的点,传输通道看作边,而传输通道的容量上限对应每条边的容量,那么以太的传输方案应该恰好为 $s$ 到 $t$ 的最大流。
虽然没有任何人能保证闯入末日塔之后就一定能将其破坏,但作为勇闯末日塔小队的先锋,你还是想在出发之前计算一下,如果成功破坏了所有将要闯入的末日塔,传输网络单位时间的最大传输量将会降至多少。
- 如果成功破坏了选择的末日塔,与其相连的所有传输通道的容量都将降至 $0$,其余传输通道容量不发生变化;此时传输网络会自动调节至一个在新的网络中传输量最大的新方案。
- 在最理想的情况下,小队将有机会调查并破坏 $L$ 座末日塔。因此,需要事先选择 $L$ 座末日塔(均不能是 $s$ 或 $t$),使得当这 $L$ 座末日塔都被成功破坏时,传输网络的新的传输方案的以太传输量尽可能地小。
输入格式
从标准输入读入数据。
输入的第一行包括五个正整数 $N, M, L, s, t$($3\le N\le 1000$,$2\le M\le \frac{N(N-1)}{2}$,$1\le L\le \min\{8,N-2\}$,$1\le s, t\le N$),分别表示该传输网络包含的末日塔数量,传输通道数量,有机会闯入的末日塔数量,最主要的以太吸收塔的编号和中枢塔的编号。
输入的第二行包括两个实数 $R, K$($1\le R\le 10^3$,$1\le K\le 10^3$),分别表示星球的半径和计算以太容量时用到的常数。
接下来 $N$ 行,每行三个实数 $a_i, b_i, q_i$($0\le a_i\le 1$,$0\le b_i< 2$,$1\le q_i \le 10^3$),描述第 $i$ 座末日塔的信息,其中 $q_i$ 表示第 $i$ 座末日塔的传输能力, $a_i$ 和 $b_i$ 共同描述末日塔的位置:令 $\theta_i = \pi a_i$,$\varphi_i = \pi b_i$(如果你习惯使用角度制而不是弧度制,可以将 $\pi$ 改为 $180^\circ$),则 $\left(x_i, y_i, z_i\right) = \left(R \sin\theta_i \cos\varphi_i, R\sin\theta_i \sin\varphi_i, R\cos\theta_i\right)$。保证末日塔的位置各不相同。
最后 $M$ 行,每行两个正整数 $u_i, v_i$($1\le u_i, v_i\le N$),表示一条传输通道连接的两座末日塔的编号。保证同一条传输通道连接的两座末日塔不相同且不互为对跖点,没有两条传输通道连接的是相同的末日塔对,且传输网络是连通的。
保证输入的所有实数保留到小数点后第 $4$ 位。
输出格式
输出到标准输出。
输出一个实数,表示如果成功破坏了将要闯入的末日塔,新的传输网络单位时间的最大传输量。当你的输出与标准输出的相对误差或绝对误差不超过 $10^{-6}$ 时,我们认为你的输出是正确的。
样例1输入
6 11 1 1 6
1.0000 1.0000
1.0000 0.0000 10.0000
0.7500 0.2500 6.0000
0.5000 0.0000 1.0000
0.5000 0.5000 1.0000
0.2500 0.2500 6.0000
0.0000 0.0000 10.0000
1 2
1 3
1 4
2 3
2 4
3 4
3 5
3 6
4 5
4 6
5 6样例1输出
8.105694691387022样例1解释
以太传输网络如下图所示。图中蓝色球面即为星球表面;紫色点为各末日塔,其中 $P_i$ 对应输入的第 $i$ 座末日塔;黄色的线表示各传输通道。
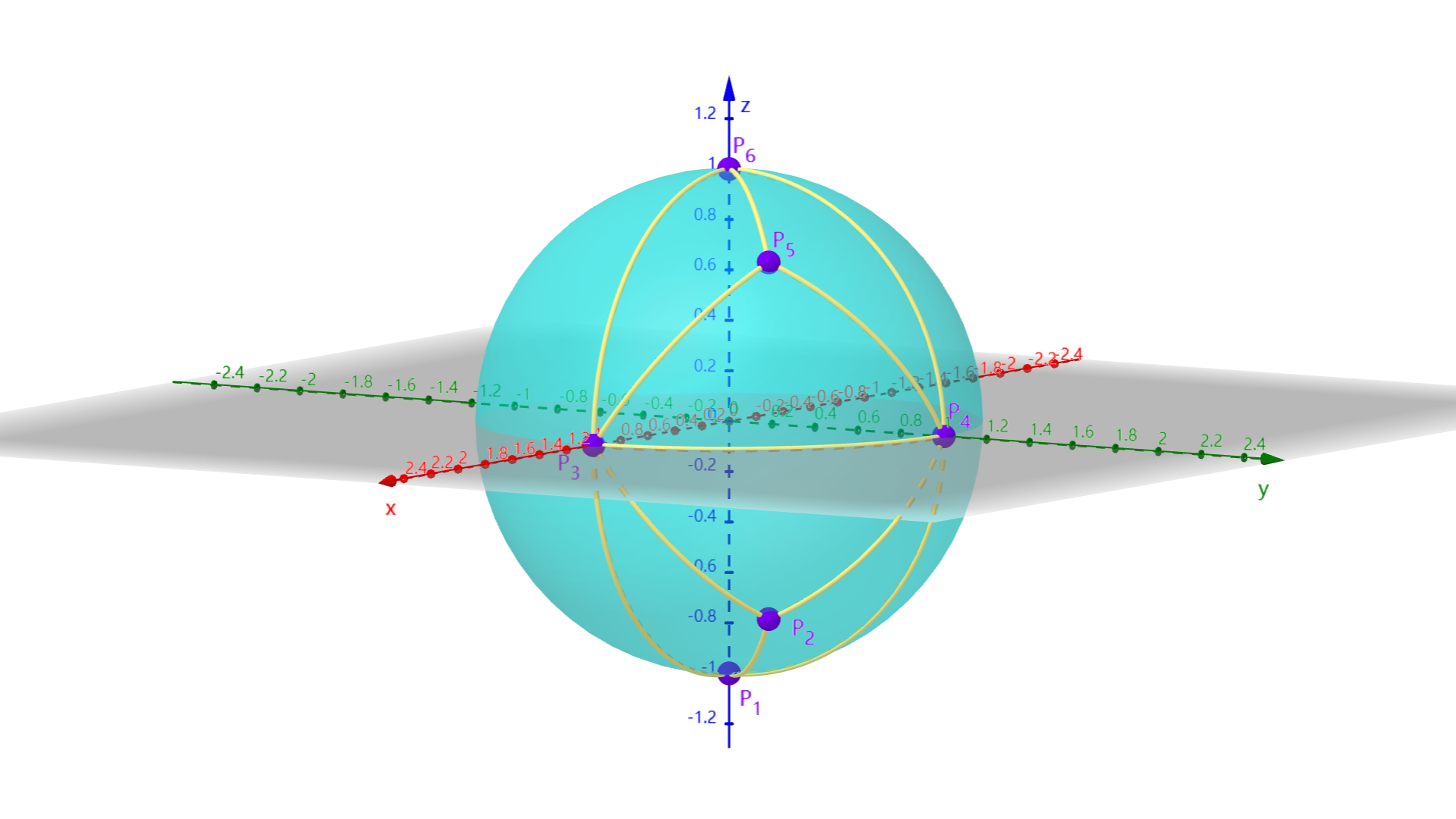
原来的传输网络单位时间最大传输量为 $188/\pi^2$。破坏第 $2$ 个末日塔或第 $5$ 个末日塔都能使新的传输网络单位时间的最大传输量降至 $80/\pi^2$,而破坏第 $3$ 个末日塔或第 $4$ 个末日塔只能使新的传输网络单位时间的最大传输量降至 $94/\pi^2$,所以应该选择第 $2$ 个或第 $5$ 个末日塔尝试破坏。
样例2
见题目目录下的 2.in 与 2.ans。
提示
在三维空间中,我们可以用一个有序的实数三元组 $(x, y, z)$ 来描述一个点的位置,其中 $x, y, z$ 分别称作这个点的横坐标、纵坐标和竖坐标。
三维空间中一个球心在 $\left(x_0, y_0, z_0\right)$、半径为 $R$ 的球面是指空间中所有满足 $\left(x-x_0\right)^2 + \left(y-y_0\right)^2+\left(z-z_0\right)^2=R^2$ 的点 $(x,y,z)$ 构成的点集。对于该球面上给定的两个不同点 $\left(x_1, y_1, z_1\right), \left(x_2, y_2, z_2\right)$,
如果它们不是一对对跖点(两个点是对跖点当且仅当它们在空间上的欧氏距离为 $2R$;也称对径点),则它们和球心不在同一直线上,这三个点唯一确定了一个平面。这个平面与球面的交线被称作“大圆”(great circle)。大圆的弧被这两个点分成了两个部分,其中较短部分的长度称为这两点在该球面上的距离。
如果两个点是对跖点,则定义它们在球面上的距离为 $\pi R$。
尽管本题不提供直接的可视化工具,但是你仍然可以用下发文件中的 convert.py,将满足本题输入格式的文件转换为可以直接输入至 Geogebra 的绘图指令。convert.py 将从标准输入读入数据,并将转换后的绘图指令输出到标准输出。例如,运行 convert.py,并将输入重定向到 1.in,程序输出如下:
$ python convert.py < 1.in
======= Commands begin =======
x^2+y^2+z^2=1^2
towers = {(1; 0.0 pi; -0.5000 pi), (1; 0.25 pi; -0.2500 pi), (1; 0.0 pi; 0.0000 pi), (1; 0.5 pi; 0.0000 pi), (1; 0.25 pi; 0.2500 pi), (1; 0.0 pi; 0.5000 pi)}
ulist = {1, 1, 1, 2, 2, 3, 3, 3, 4, 4, 5}
vlist = {2, 3, 4, 3, 4, 4, 5, 6, 5, 6, 6}
Zip(CircularArc(O, A, B), A, Zip(towers(i), i, ulist), B, Zip(towers(i), i, vlist))
Sequence(Text("Tower " + (i), towers(i), true), i, 1, 6)
======= Commands end =======将 ======= Commands begin ======= 与 ======= Commands end ======= 之间的每行指令依次粘贴至代数区的输入框中,即可得到与样例 1 附图中类似的三维对象。你可能需要 安装 Python 3.6 或更高版本来运行 convert.py。
这个转换工具,无疑是善良的出题人无私的馈赠。出题人相信,这个美妙的转换工具,可以给拼搏于 AC 这道题的逐梦之路上的你,提供一个有力的援助。