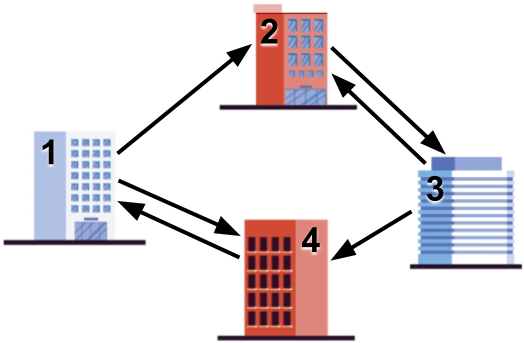
Gooli is a huge company that owns $\mathbf{B}$ buildings in a hilly area, numbered $1$ through $\mathbf{B}$. Six years ago, Gooli built slides that allowed employees to go from one building to another. Each slide allows anyone to go from the slide's origin building to the slide's destination building, but not the other way around. Gooli's CEO is very proud of their slides and wants to organize a parade through the slides. She has tasked Melek, Gooli's Head of Transportation and a problem-solving enthusiast, with designing the parade's route.

She has some requirements for the parade route in mind:

• It must start and end at building $1$, where her office is located.
• It must visit each building the same number of times. Being in building $1$ at the start of the route does not count as a visit.
• It must use each slide at least once.
• It must have at most $10^6$ steps.

Given the layout of buildings and slides, help Melek find a route that satisfies all of the CEO's requirements, if one exists.

Input

The first line of the input gives the number of test cases, $\mathbf{T}$. $\mathbf{T}$ test cases follow. Each test case starts with a line containing two integers $\mathbf{B}$ and $\mathbf{S}$: the number of buildings and slides, respectively. Then, $\mathbf{S}$ lines follow. The $i$-th of these lines contains two integers $\mathbf{U_i}$ and $\mathbf{V_i}$, indicating that the $i$-th slide goes from building $\mathbf{U_i}$ to building $\mathbf{V_i}$.

Output

For each test case, output one line containing Case #x: y, where $x$ is the test case number (starting from 1). If there is no route that fulfills all the requirements, $y$ must be IMPOSSIBLE. If there is, $y$ must be an integer between $\mathbf{S}+1$ and $10^6+1$, inclusive, representing the length of one such route you want to exhibit. In that case, output another line containing $y$ integers $z_1\ z_2\ \dots\ z_y$, where $z_j$ is the $j$-th building in your proposed route. Notice that $z_1 = z_y = 1$ and that each building must appear the same number of times among the $z_j$, except for building $1$, which appears exactly one extra time.

Limits

Memory limit: 1 GB.

• $1 \le \mathbf{T} \le 100$.
• $1 \le \mathbf{U_i} \le \mathbf{B}$, for all $i$.
• $1 \le \mathbf{V_i} \le \mathbf{B}$, for all $i$.
• $\mathbf{U_i} \ne \mathbf{V_i}$, for all $i$.
• $(\mathbf{U_i}, \mathbf{V_i}) \neq (\mathbf{U_j}, \mathbf{V_j})$, for all $i \neq j$.

Test Set 1 (Visible Verdict) (11 points)

Time limit: 10 seconds.

• $2 \le \mathbf{B} \le 10$.
• $2 \le \mathbf{S} \le 10$.

Test Set 2 (Hidden Verdict) (24 points)

Time limit: 20 seconds.

• $2 \le \mathbf{B} \le 200$.
• $2 \le \mathbf{S} \le 5000$.

Sample

Input

5
2 2
2 1
1 2
3 4
2 3
1 2
3 2
1 3
3 6
1 2
1 3
2 1
2 3
3 1
3 2
3 4
1 2
2 1
1 3
3 1
4 6
1 2
1 4
2 3
3 2
3 4
4 1

Output

Case #1: 7
1 2 1 2 1 2 1
Case #2: IMPOSSIBLE
Case #3: 7
1 2 3 1 3 2 1
Case #4: IMPOSSIBLE
Case #5: 9
1 4 1 2 3 2 3 4 1

In Sample Case #1, another acceptable parade route is one that goes from building $1$ to building $2$ and then back for a total of $2$ steps.

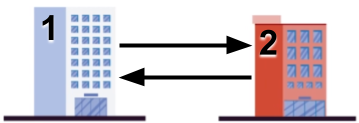
In Sample Case #2, there are no slides leading to building $1$, so no valid parade can exist.

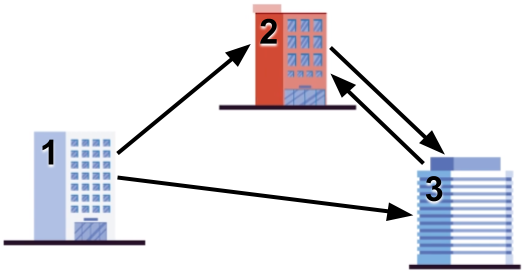
In Sample Case #3, the parade route the sample output exhibits goes through each building twice.

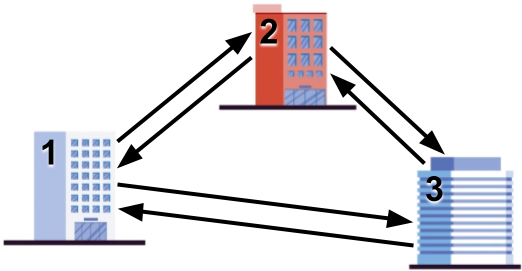
Sample Case #4 is pictured below.

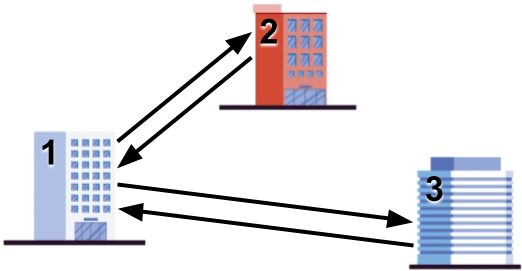
Sample Case #5 is the one illustrated in the problem statement. In the parade route in the sample output, the slides from $2$ to $3$ and from $4$ to $1$ are used twice, but the rest of the slides are used only once each.