Plansza do gry "w kółko" składa się z $m$ pól umieszczonych na okręgu i ponumerowanych kolejno liczbami od $1$ do $m$. Na planszy rozmieszczonych jest $b$ białych i $c$ czarnych pionków, na każdym polu co najwyżej jeden. W grę gra dwóch graczy, biały i czarny. Począwszy od białego, gracze na przemian wykonują ruchy na planszy. Ruch polega na przesunięciu wybranego pionka swojego koloru o dowolną liczbę niezajętych pól w przód albo w tył. Przykładowo, na poniższej planszy gracz biały może wykonać ruch pionkiem z pola 3 na pole 4 lub pionkiem z pola 8 na jedno z pól 7, 9, 1.
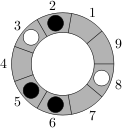
Jeśli w swojej turze gracz nie może wykonać żadnego ruchu, przegrywa. Wiedząc, że obaj gracze grają optymalnie, sprawdź, który z nich wygra. Może się tak zdarzyć, że żaden z graczy nie wygra (gra będzie toczyła się w nieskończoność).
Wejście
W pierwszym wierszu standardowego wejścia znajduje się jedna liczba $t$ oznaczająca liczbę plansz do rozpatrzenia. W kolejnych wierszach znajdują się opisy poszczególnych plansz; każdy z nich składa się z trzech wierszy. W pierwszym znajdują się trzy liczby całkowite $m$, $b$ i $c$ ($1 \le m \le 10^9$, $1\le b,c$) pooddzielane pojedynczymi odstępami i oznaczające długość planszy, liczbę białych pionków i liczbę czarnych pionków. W drugim wierszu znajduje się rosnący ciąg $b$ liczb (z przedziału od $1$ do $m$) określający położenia białych pionków. W trzecim wierszu znajduje się rosnący ciąg $c$ liczb określający położenia czarnych pionków. Sumaryczna liczba pionków na wszystkich planszach nie przekracza $10^6$.
Wyjście
Na standardowe wyjście należy wypisać dokładnie $t$ wierszy z odpowiedziami dla kolejnych plansz. Odpowiedzią jest jeden znak B, C lub R, w zależności od tego, czy wygrywa gracz biały, czarny, czy też gra toczy się w nieskończoność.
Przykład
Dla danych wejściowych:
3
9 2 3
3 8
2 5 6
6 2 2
5 6
2 4
7 1 1
3
4poprawną odpowiedzią jest:
C
B
RAutor zadania: Tomasz Idziaszek.