蜘蛛爬树 - 题目

问题描述

小 F 在自家院子里种了一棵 $n$ 个节点的树。节点编号为 $1$ 到 $n$。有 $n-1$ 条边将这些节点连接起来，第 $i$ 条边连接节点 $u_i$ 与节点 $v_i$，长度为 $w_i$。

接下来的几天中，小 F 将这棵树复制了 $m-1$ 份并排成一排，于是他拥有了 $m$ 棵完全相同的树。第 $k$ 棵树节点 $x$ 的编号为 $(k-1)\times n+x$。为方便叙述，下面用二元组 $(k,x)$ 表示编号为 $(k-1)\times n+x$ 的节点。

小 F 的院子里有 $q$ 只蜘蛛。这些蜘蛛会对于任意 $1\le k < m,1\le x\le n$，用一条蛛丝将 $(k,x)$ 与 $(k+1,x)$ 连接起来。

由于每个节点的高度和脆弱程度不同，这些蛛丝之间可能会有长短。但是由于这些树完全相同，且相邻树之间的距离相同，所以对于任意 $1\le k_1,k_2 < m,1\le x\le n$，连接 $(k_1,x)$ 与 $(k_1+1,x)$ 的蛛丝长度等于连接 $(k_2,x)$ 与 $(k_2+1,x)$ 的蛛丝长度。

于是我们可以用一个序列 $a_1,a_2,\ldots,a_n$ 来描述这些蛛丝，其中 $a_x$ 表示对于任意 $1\le k < m$，连接 $(k,x)$ 与 $(k+1,x)$ 的蛛丝长度。

为了检验成果，蜘蛛们展开了一场爬树比赛。第 $j$ 只蜘蛛要从节点 $s_j$ 沿树边和蛛丝爬到节点 $t_j$。

你需要帮蜘蛛们算一算，每只蜘蛛的最短路径长度。

输入格式

第一行三个整数 $n,m,q$，分别表示每棵树的节点树、树的数量和蜘蛛数量。

第二行 $n$ 个整数 $a_1,a_2,\ldots,a_n$，描述蛛丝长度。

接下来 $n-1$ 行，第 $i$ 行三个整数 $u_i,v_i,w_i$，描述第 $i$ 条边。

接下来 $q$ 行，第 $j$ 行两个整数 $s_j,t_j$，表示第 $j$ 只蜘蛛的起点和终点。

输出格式

输出 $q$ 行，第 $j$ 行一个整数，表示第 $j$ 只蜘蛛的最短路径长度。

样例输入

样例输出

11
9

样例解释

$3$ 棵树与蛛丝形成的结构如下（黑线表示树边，蓝线表示蛛丝）：

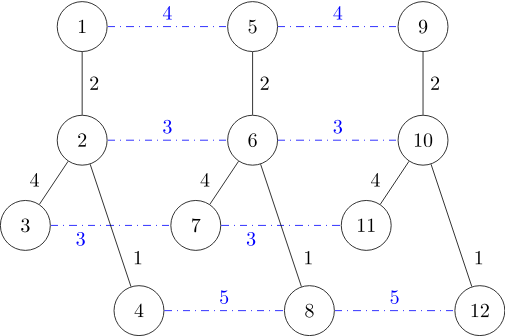
第 $1$ 只蜘蛛的一条最短路径如红色带箭头路径所示：

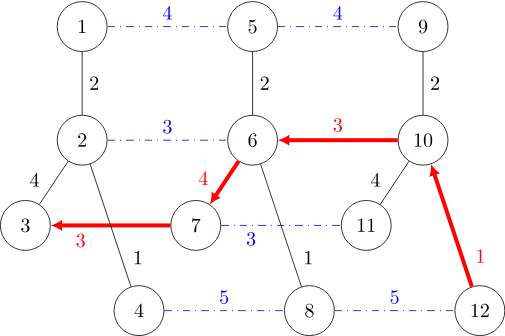
第 $2$ 只蜘蛛的一条最短路径如红色带箭头路径所示：

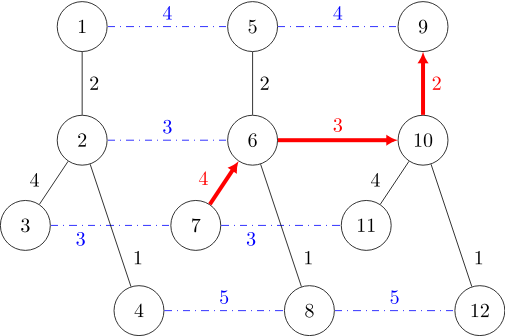
数据规模与约定

子任务 $1\ (3\text{ pt})$：$n\le 100,m\le 100,q\le 1000$
子任务 $2\ (5\text{ pt})$：$n,q\le 5000$
子任务 $3\ (11\text{ pt})$：$m\le 20$
子任务 $4\ (12\text{ pt})$：树是一条链
子任务 $5\ (9\text{ pt})$：树是一个菊花
子任务 $6\ (22\text{ pt})$：$s_j=1$
子任务 $7\ (18\text{ pt})$：$n,q\le 5\times 10^4$
子任务 $8\ (20\text{ pt})$：无附加限制

对于 $100\%$ 的数据，$1\le n,q\le 2\times 10^5,1\le m\le 10^9,1\le a_x\le 10^9,1\le w_i\le 10^{12},1\le u_i,v_i\le n,1\le s_j,t_j\le n\times m$。

QOJ.ac

QOJ

2021 集训队互测 Round 12