题目背景
在精心地规划完工人的移动路线,执行完所有计划之后,你终于有钱了。你承包下了一个更大的矿坑,并购买了更先进的设备。
但是开始运行了你才发现,一部分运输矿物的通道居然装反了!还好它们本来就是可以反向的,并且中控的系统可以让你轻易地操作。
然而,现在最大的问题是,你刚刚接手这个矿坑,你甚至连它长什么样都不知道,也就更不知道每个开关是对应哪一条运输通道的。
时间就是金钱,你想要尽快摸清整个矿坑的结构以及所有开关与通道的对应关系。
题目描述
这是一道交互题。
已知你的矿坑有 n 个节点,编号为 1∼n。它们通过 n−1 条运输通道连成一个树形结构。
运输通道都是单向的。对于一条从节点 u 到节点 v 的运输通道,可以将所有由节点 u 产出的矿或运送到节点 u 的矿以较快的速度运送到节点 v。如果一个节点有多条以其为起点的运输通道,那么会把这些矿平均分配给这些运输通道。
中控的系统包含 n−1 个开关和一个监视器。开关的编号为 1∼n−1,每个开关可以拨到 0 或 1 的位置。n−1 个开关和 n−1 条运输通道一一对应,但你并不知道它们的对应关系。你只知道,假设编号为 i 的开关对应的运输通道在被装上去时是从 ui 到 vi 的,那么当开关拨到 0 的时候,它的运输方向和它被装上去时相同;当开关拨到 1 的时候,它的运输方向会变成从 vi 到 ui。你的监视器可以监控到达每个节点的矿分别来自多少个不同的节点,也就是说,有多少个节点(包括其本身)能够通过运输通道把矿运输到这个节点。
当你调整完开关的位置后,需要等一段时间,监视器的结果才会趋于稳定,这时你的读数才是有意义的。所以为了避免浪费太多时间,你希望在 50 次读数之内确定你想知道的所有信息。
输入格式
从标准输入读入数据。
开始时你需要输入一个正整数 n。保证 2≤n≤10000。
之后的输入会基于你的输出生成读数。你的读数结果是一行 n 个正整数,其中第 i 个表示到达节点 i 的矿来自多少个不同的节点。
每个测试点中,矿坑的连接方式和所有运输通道刚装上去时的方向都是固定的,也就是说,这些不会因为你的输出而动态修改为另外一种符合之前所有回答的方案。
输出格式
输出到标准输出。
当你需要调整开关并等待读数时,输出一行 ? s,其中 s 为一个长为 n−1 的 01 串,其中第 i 位表示编号为 i 的开关拨到的位置。然后交互库会在你的标准输入中给出监视器趋于稳定之后的读数结果。你最多只能读数 50 次。
当你已经知道了所有通道的信息时,输出一行 ! u1 v1 ... un-1 vn-1,其中 ui,vi 表示编号为 i 的开关对应的运输通道被装上去时的方向是从节点 ui 到节点 vi 的。
在输出一行之后,你需要刷新输出缓冲区,否则评测结果可能会变成 TLE。刷新输出缓冲区的方式为:
C:
fflush(stdout);C++:
fflush(stdout);或std::cout.flush();或使用std::endl换行Java:
System.out.flush();Python:
sys.stdout.flush()
样例
Input: Output:
5
? 0110
1 4 1 2 3
? 0000
1 1 2 3 4
! 1 4 2 3 2 4 4 5解释
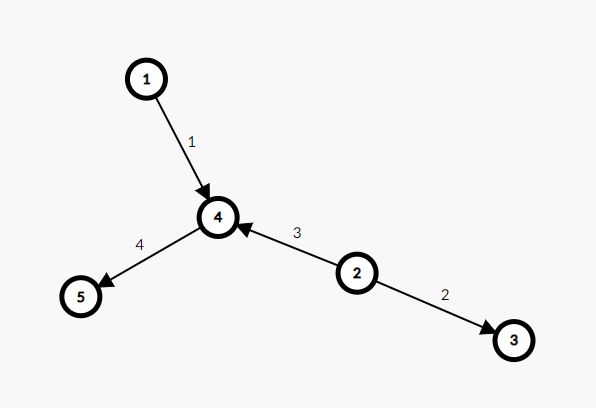
通道的初始方向如上图所示。通道上的数字代表和通道对应的开关的编号。
样例只是用来说明输入输出格式和读数结果,并不意味着这次读数能够推出答案。
评分方式
交互库的运行时间和内存不计入时间和内存限制。
若超出读数次数限制、最后的回答错误或输出格式错误,评测结果均为 WA。