伸展树 - Problem

伸展树（Splay）是一种平衡二叉搜索树。也就是说，伸展树首先是一棵二叉树：每个节点至多有两个孩子（左孩子、右孩子）。

伸展树中有两种基本操作：左旋和右旋。其中，左旋是把节点的右孩子上提，右旋是把节点的左孩子上提。

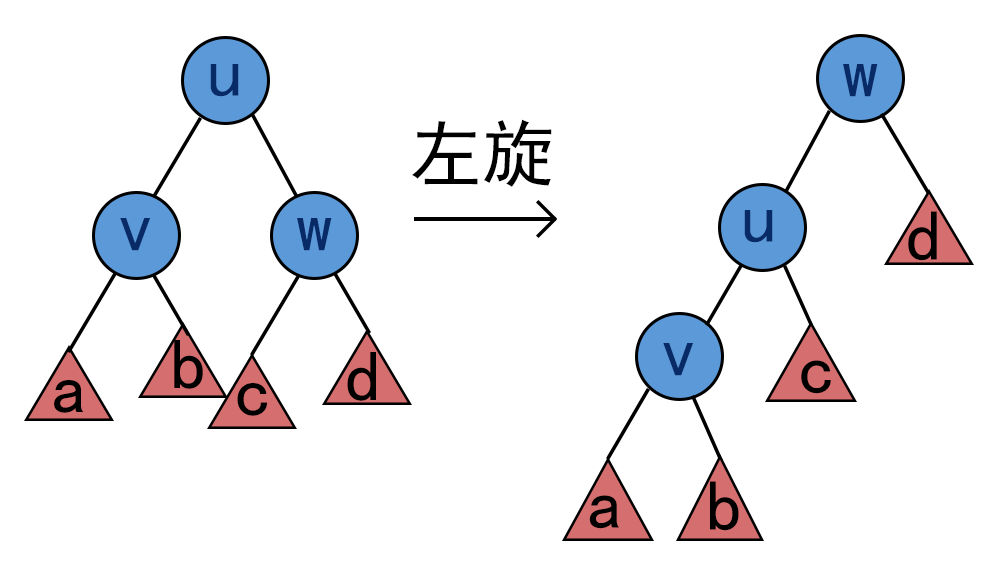
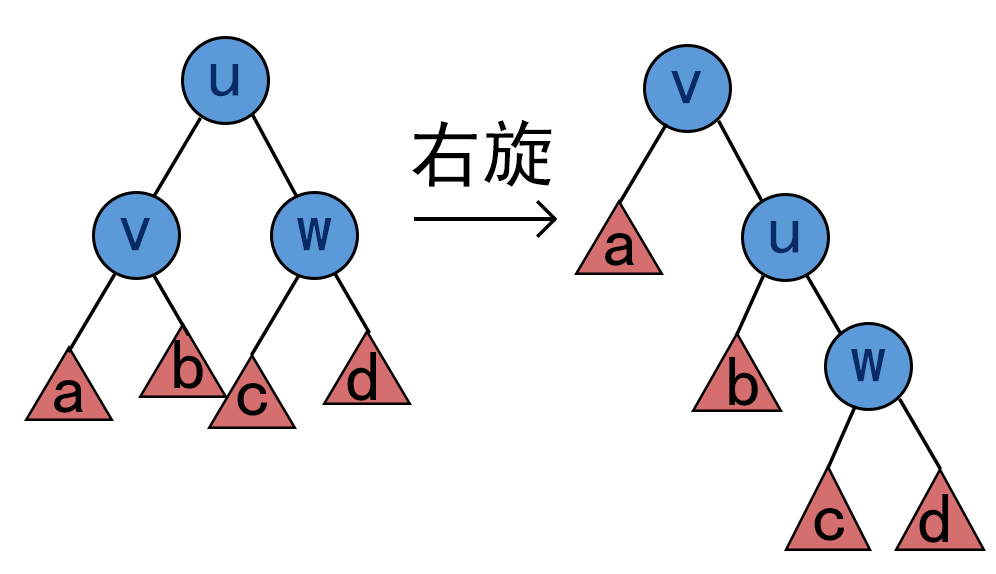
你现在有两棵有标号的、节点数为 $n$ 的伸展树，你需要用至多 $2n$ 次左旋或右旋操作把初始状态变成目标状态。

从标准输入读入数据。

第一行一个正整数 $n$ 表示节点个数。

接下来 $n-1$ 行，每行 $3$ 个数字 $x,y,c$，表示 $x$ 节点有孩子节点 $y$，如果 $c$ 为 $0$，则 $y$ 为左孩子，否则为右孩子。这棵树是初始状态。

再接下来 $n-1$ 行，每行 $3$ 个数字 $x,y,c$，表示 $x$ 节点有孩子节点 $y$，如果 $c$ 为 $0$，则 $y$ 为左孩子，否则为右孩子。这棵树是目标状态。

输出到标准输出。

首先第一行输出 No 或 Yes，No 表示不能通过至多 $2n$ 次操作得到目标状态，否则输出 Yes。

如果输出 Yes，则接下来一行输出一个整数 $times$，表示你的构造方案中所用的操作次数。

接下来 $times$ 行，每行两个整数 $x,c$，如果 $c$ 为 $0$，那么表示对节点 $x$ 左旋，否则是右旋。

保证输入的树合法。

2
1 2 0
2 1 0

No

保证 $1\le n \le 10^6$。

子任务 1（30 分）：$n\le 10$。

子任务 2（30 分）：$n\le 1000$。

子任务 3（40 分）：$n\le 10^6$。

QOJ.ac