题目背景
在地底的洞府中住着一个霍比特人。这不是那种让人恶心的洞,脏兮兮湿乎乎的,长满虫子,透着一股子泥腥味儿;也不是那种满是泥沙的洞,干巴巴光秃秃的,没地方好坐,也没好东西好吃。这是一个霍比特人的洞,而霍比特人的洞就意味着舒适。
——《霍比特人》开篇
题目描述
白兰地厅是最大的霍比特洞之一,位于雄鹿山内部,是白兰地鹿家族的祖宅,数百年来白兰地鹿家族的霍比特人不断扩张白兰地厅的规模,直至其占满了整个山丘。白兰地鹿家族是弗罗多·巴金斯的母族,他十二岁那年,双亲在划船时不幸溺亡,弗罗多便被交由白兰地厅抚养。
白兰地厅有 $n$ 个房间,房间之间以双向圆形通道相连。从任意一个房间出发都可以到达任意另一个房间,但为了避免人们迷失在交错纵横的通道里,白兰地厅经过了精心设计,以保证任意两个房间之间仅有一条路径可达。在炎炎的夏日,白兰地鹿家有贮藏甘甜可口的西瓜的习俗,但由于西瓜个头太大,白兰地鹿家会在每个房间里贮藏恰好一个西瓜。对一个西瓜而言最重要的是它的甜度,$i$ 号房间里的西瓜的甜度为 $a_i$。
弗罗多算是客居于此,因而可以在白兰地厅自由走动,也可以在任意一个他想过夜的房间里过夜。弗罗多每天会从一个房间前往另一个房间,但他生性懒惰,总是会沿着最短的路径来走。经过每个房间时弗罗多都可以品尝那个房间里的西瓜,当然他也可以只是经过而选择忽略西瓜——这也包括了他出发和最终落脚的房间。
弗罗多喜欢吃甜的西瓜,然而众所周知,味蕾感受到的甜度是相对甜度,也就是说,如果弗罗多先吃了一个甜度为 $x$ 的西瓜,紧接着又吃了一个甜度为 $y$ 的西瓜,当 $y > x$ 时,味蕾才会觉得后者是甜的,当 $y \le x$ 时,弗罗多并不会感觉到后者的甜。所以,弗罗多给自己定了一个规矩:除了每天的第一个西瓜外,他吃的每一个西瓜的甜度都要大于前一个。
一天清晨,弗罗多突然对白兰地厅里百无聊赖的生活心生倦意,或许只有西瓜才能让他解忧,他想吃很多个西瓜,并且不想违背他的规矩。弗罗多不禁陷入思考……他的一天里总是面临很多选择,从哪一个房间出发、最终抵达哪一个房间、在经过的房间中选择吃哪一些房间的西瓜、并忽略另一些房间里的西瓜……弗罗多想知道,在如此多的选择下,弗罗多的一天最多能吃到多少个西瓜呢?
输入格式
从标准输入读入数据。
第一行包含一个正整数 $n$,表示白兰地厅的房间数量。保证 $2 \le n \le 10^{5}$。
第二行包含 $n$ 个正整数,第 $i$ 个整数为 $a_i$,表示 $i$ 号房间里的西瓜的甜度。保证 $1 \le a_i \le 10^{9}$。
接下来 $n - 1$ 行描述了白兰地厅的形态,第 $i$ 行为两个正整数 $u_i$ 和 $v_i$,表示 $u_i$ 号房间和 $v_i$ 号房间之间有一条双向通道。保证 $1 \le u_i, v_i \le n$。
输出格式
输出到标准输出。
输出共一行,包含一个正整数,即 弗罗多一天里最多能吃到多少个西瓜。
样例
输入
9
2 4 1 6 7 3 5 1 2
2 3
6 1
6 7
1 2
8 6
4 2
6 9
4 5输出
5解释
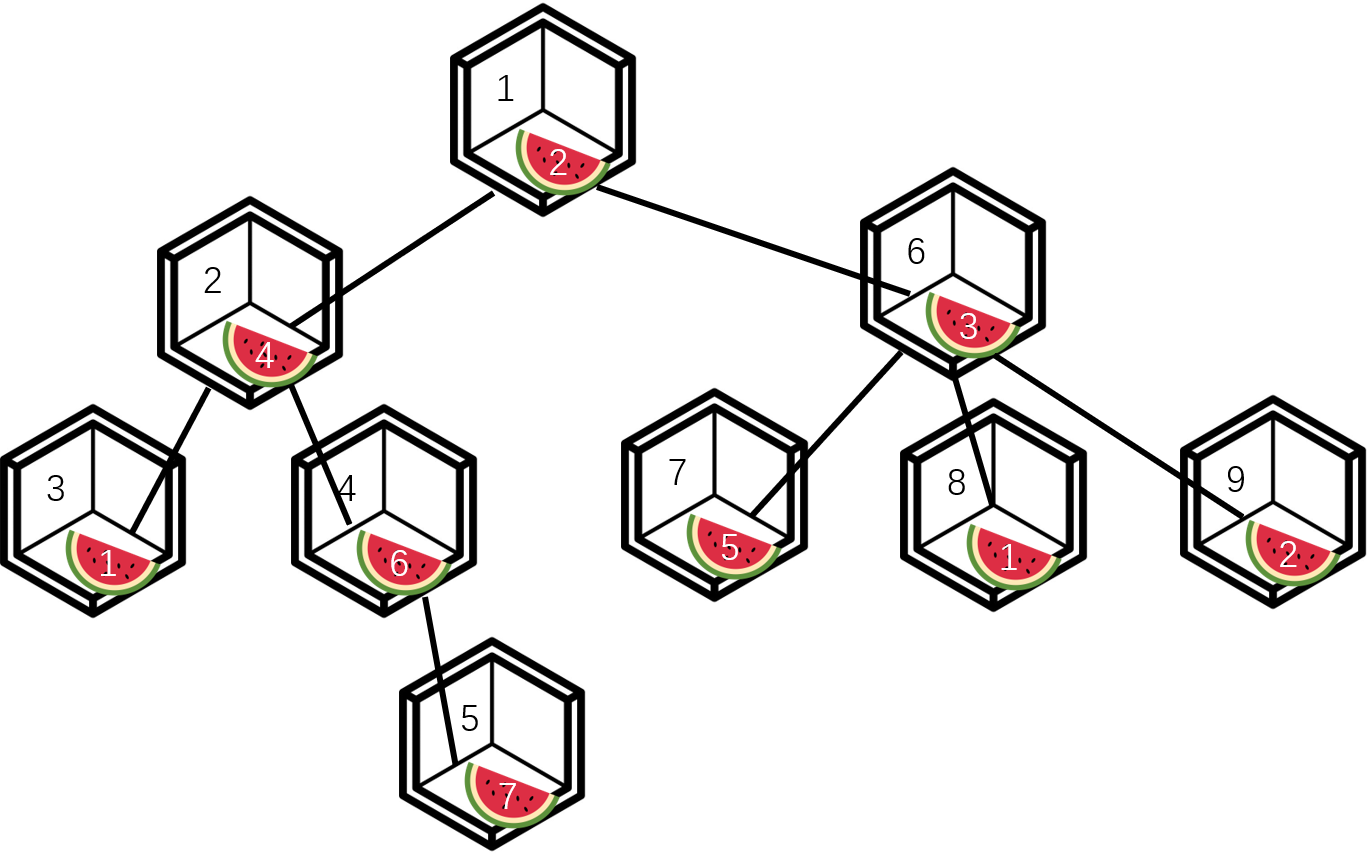
下图为本样例中的白兰地厅的示意图。黑色直线表示房间之间的通道;左侧墙壁上的数字为房间编号;西瓜内部的数字为其甜度。
弗罗多一天最多能吃到 5 个西瓜,有三种选择可以让他吃到 5 个西瓜。
选择一:
- 从 8 号房间出发,并吃掉房间里的西瓜(甜度为 1);
- 经过 6 号房间,忽略房间里的西瓜;
- 经过 1 号房间,并吃掉房间里的西瓜(甜度为 2);
- 经过 2 号房间,并吃掉房间里的西瓜(甜度为 4);
- 经过 4 号房间,并吃掉房间里的西瓜(甜度为 6);
- 抵达 5 号房间,并吃掉房间里的西瓜(甜度为 7)。
选择二:
- 从 8 号房间出发,并吃掉房间里的西瓜(甜度为 1);
- 经过 6 号房间,并吃掉房间里的西瓜(甜度为 3);
- 经过 1 号房间,忽略房间里的西瓜;
- 经过 2 号房间,并吃掉房间里的西瓜(甜度为 4);
- 经过 4 号房间,并吃掉房间里的西瓜(甜度为 6);
- 抵达 5 号房间,并吃掉房间里的西瓜(甜度为 7)。
选择三:
- 从 9 号房间出发,并吃掉房间里的西瓜(甜度为 2);
- 经过 6 号房间,并吃掉房间里的西瓜(甜度为 3);
- 经过 1 号房间,忽略房间里的西瓜;
- 经过 2 号房间,并吃掉房间里的西瓜(甜度为 4);
- 经过 4 号房间,并吃掉房间里的西瓜(甜度为 6);
- 抵达 5 号房间,并吃掉房间里的西瓜(甜度为 7)。
样例二
见下载目录下的 ex_2.in 与 ex_2.ans。
子任务
本题有多个子任务,每个子任务可能包含多个测试点,只有通过了一个子任务中的所有测试点才能得到该子任务的分数。
每个子任务的测试点满足一些特殊的限制,具体如下表:
| 子任务编号 | $n \le$ | 特殊性质 | 占分 |
|---|---|---|---|
| 1 | 100 | 无 | 10 |
| 2 | 1000 | ||
| 3 | 5000 | $a_i \le 4$ | |
| 4 | 100000 | $a_i \le 2$ | |
| 5 | 树中仅有一个节点度数大于 1 | ||
| 6 | 树中所有节点度数不超过 2 | ||
| 7 | 无 | 40 |
对于所有测试点,保证 $1 \le a_i \le 10^{9}$,$2 \le n \le 10^{5}$。