本题数据经过加强。
由于数据资源限制,并没有把让 std 跑满的全部极限数据挂入正式数据中。std 在现行数据下只用跑 6.36s 左右,请留意。但这并不意味着复杂度错误的做法总能通过本题。
如果想不出正解可以先从某几个特殊性质入手哦。
题目背景
在那灰暗的塔楼前,对立见到了些许光芒碎片。
那些光芒碎片萦绕在对立身旁,宛如繁花点缀。
步入那扭曲的迷宫,对立试图收集其中的纷争碎片,并尝试摧毁这个迷宫。
对立的身旁充斥着光芒和纷争碎片,交错纷飞。
终于,对立来到了那迷宫的最深处。
在那片形状极其古怪的记忆残片上,反射的,是一个世界走向灭亡的回忆。
末日来临,天空撕裂,大地崩坠。
由于这块残片上所承载的「能量」实在过于巨大,对立试图使用其身旁的光芒和纷争碎片来缓和这份巨大的精神上的冲击。
具体的,这块扭曲的残片形成一个「树」的结构,对立将在树的每条边上放上一片光芒或者纷争碎片。
对立将会把这颗树上的边切割成若干条链,使得最终每条边恰好属于其中的某一条链。由于残片的特殊结构,树上的一个节点可以同时属于多条链。
对立会取出一部分链,将放置碎片相同的前缀段进行合并,最后形成一颗新的树,也就是所谓的「Trie 树」。
这颗新的树上的节点越多,就越能缓和对立的情绪,让其冷静下来。
在疯狂中,对立已经给残片上的某些边放上了光芒碎片或者纷争碎片。
一刹那的清醒间,对立意识到了些许不对。因此对立还可以往剩下的边上任意选择光芒或者纷争碎片。
在恍惚间,对立发现自己并不知道如何放置并切割是最优的。
思绪飞快地运转起来。怎样是最优的呢?
相信你已有答案。
题目描述
给定一颗 n 个节点的树,节点编号 0∼n−1。
边有边权,边权一般为 0 或者 1;但有的边的边权还未确定。
你要给每条未被确定边权的边确定一个 0 或者 1 的边权,然后从树上取出若干条有向路径,使得这些链两两之间满足边不相交。
然后你会把这些路径插入一颗 0/1-Trie,你希望最大化这颗 0/1-Trie 上的节点数。(由于 0/1-Trie 的定义较为简单,参加胡策的各位同学应该都知道,这里就不作详述了)
你可能需要构造具体的选择方案。
输入格式
本题每个测试点中有多组测试数据。
第一行两个整数 T,o,其中 T 表示测试数据组数,o 表示该测试点的一些特殊性质(请参见「数据范围与提示」一节的描述)。
接下来有 T 组测试数据。
每组数据第一行一个整数 n,表示点的个数。
接下来 n−1 行,每行三个整数 u,v,w,表示一条连接点 u,v 的边。当 0≤w≤1 时,表示这条边边权为 w;否则总有 w=2,表示这条边的边权还未确定。
保证这些边形成一颗点集为 0∼n−1 的树。
输出格式
开头应当输出一个数 c(c∈{0,1}),表示你是否选择在该测试点输出方案,我们会使用 Special Judge 来校验你的输出是否正确。注意这将影响你在该测试点的得分上限,详见「数据范围与提示」一节的描述。
对于每组测试数据,首先输出一行一个数 A,表示该组数据的答案。
当 c=1 时,还需要继续按如下格式输出你所构造的方案:
- 先输出一行一个数 m,表示你构造的方案中路径的数目。
- 接下来一行 n−1 个数,每个数为 0 或者 1,表示按输入顺序各边的边权。对于边权本身已经确定的边,请原样输出。
- 接下来 m 行,每行两个数 u,v,表示树上一条从 u 到 v 的路径。要求 u≠v,且路径两两边不相交。
输入输出样例
因为本题数据规模太大,直接提交评测会对评测机带来很大压力,本题将提供很多大样例;请尽量减少本题的提交次数。
请参见下发文件 axiumcrisis*.in/ans,共 20 组,基本按照部分分的方法造。
注意下发的答案文件中没有给出构造方案,仅会给出每组数据的答案。
下发了一个 checker.cpp,你可以自行编译并在终端运行校验合法性。具体使用方法请参考「数据范围与提示」一节的描述。正式测评时使用的 Special Judge 与其并不相同。
为了方便你更好地理解题意,此处额外附一个手搓的样例,这份样例未被放入下发文件。
建议使用该组样例及样例解释校验你对题意的理解,以免误读。
样例输入
9 0 9 1 2 1 3 4 1 5 6 1 7 8 1 2 0 0 4 0 0 6 0 0 8 0 0 9 1 2 2 3 4 1 5 6 1 7 8 1 2 0 0 4 0 0 6 0 0 8 0 0 5 1 2 2 3 4 1 0 3 1 2 3 0 17 1 2 1 2 3 0 3 4 1 4 0 0 5 6 1 6 7 0 7 8 1 8 0 0 9 10 1 10 11 0 11 12 1 12 0 0 13 14 1 14 15 0 15 16 1 16 0 0 17 1 2 1 2 0 0 3 4 1 4 0 0 5 6 1 6 0 0 7 8 1 8 0 0 9 10 1 10 11 0 11 12 1 12 0 0 13 14 1 14 15 0 15 16 1 16 0 0 17 1 2 2 2 0 2 3 4 2 4 0 2 5 6 2 6 0 2 7 8 2 8 0 2 9 10 2 10 11 2 11 12 2 12 0 2 13 14 2 14 15 2 15 16 2 16 0 2 18 1 2 1 2 0 0 3 4 1 4 0 0 5 6 1 6 0 0 7 8 1 8 0 0 9 10 1 10 11 0 11 12 1 12 0 0 13 14 1 14 15 0 15 16 1 16 0 0 0 17 2 18 1 2 2 2 0 2 3 4 2 4 0 2 5 6 2 6 0 2 7 8 2 8 0 2 9 10 2 10 11 2 11 12 2 12 0 2 13 14 2 14 15 2 15 16 2 16 0 2 17 0 2 18 1 2 2 2 3 2 3 4 2 4 5 2 5 6 2 6 7 2 7 8 2 8 9 2 9 10 2 10 11 2 11 12 2 12 13 2 13 14 2 14 15 2 15 16 2 16 17 2 17 0 2
样例输出
1 8 3 1 1 1 1 0 0 0 0 1 3 5 6 6 7 9 2 0 1 1 1 0 0 0 0 3 5 1 7 5 2 0 1 1 0 4 3 1 0 16 3 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 5 1 13 14 14 9 14 5 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 3 1 5 6 14 13 14 7 6 9 16 3 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 7 5 1 3 13 9 15 4 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 0 13 3 1 7 0 5 17 9 16 4 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 1 7 17 0 5 3 13 9 18 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0
样例答案
8 9 5 16 14 16 15 16 18
样例解释
样例输出即 .out 文件,也就是你要输出的结果,在 c=1 时需要构造一组合法方案。
样例答案即 .ans 文件,该文件中仅会给出每组数据的答案,不会给出构造方案。
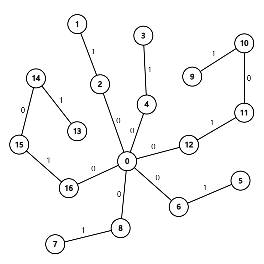
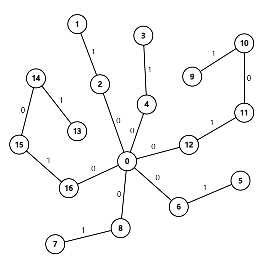
接下来依次附上这 9 组样例的图示(选择边权前 / 后各一张)。
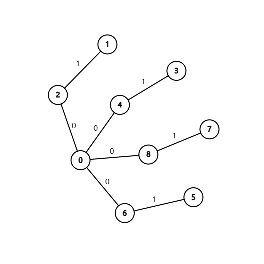
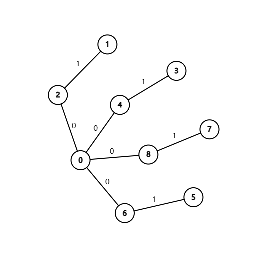
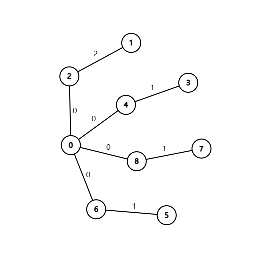
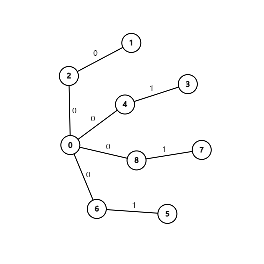
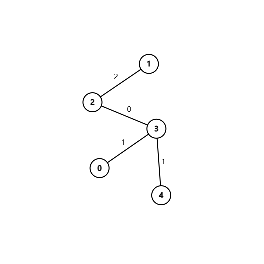
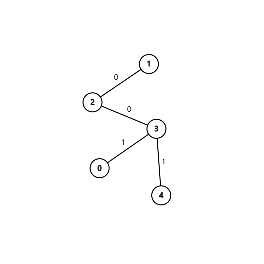
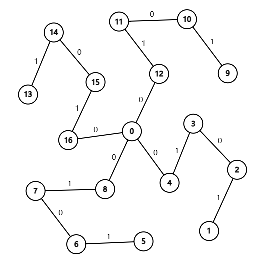
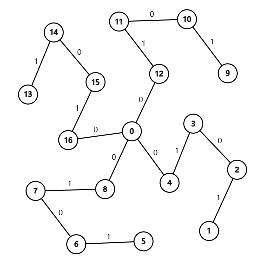
数据范围与提示
对于所有的数据,保证 2≤n≤18,1≤T≤3000。
本题设置子任务,各子任务共 20 个测试点。具体的测试点分布可以见下表。其中形如 (l,r) 的一列对应的数据表示 l≤n≤r 的数据组数,「无限制」表示无额外限制。o 的含义将在之后注明。
| 测试点编号 | (2,4) | (5,6) | (7,8) | (9,11) | (12,14) | (15,17) | (18,18) | o |
|---|---|---|---|---|---|---|---|---|
| 1∼2 | ≤1000 | =0 | =0 | =0 | =0 | =0 | =0 | =0 |
| 3∼4 | 无限制 | ≤500 | ≤10 | =0 | =0 | =0 | =0 | =3 |
| 5 | 无限制 | ≤1000 | ≤50 | ≤10 | =0 | =0 | =0 | =4 |
| 6 | 无限制 | ≤1000 | ≤50 | ≤10 | =0 | =0 | =0 | =0 |
| 7∼8 | 无限制 | 无限制 | ≤1000 | ≤60 | ≤10 | =0 | =0 | =3 |
| 9 | 无限制 | 无限制 | ≤1000 | ≤60 | ≤10 | =0 | =0 | =4 |
| 10 | 无限制 | 无限制 | ≤1000 | ≤60 | ≤10 | =0 | =0 | =0 |
| 11∼12 | 无限制 | 无限制 | 无限制 | ≤300 | ≤30 | ≤10 | =0 | =3 |
| 13 | 无限制 | 无限制 | 无限制 | ≤500 | ≤40 | ≤15 | ≤5 | =1 |
| 14∼16 | 无限制 | 无限制 | 无限制 | ≤500 | ≤40 | ≤15 | ≤5 | =2 |
| 17∼18 | 无限制 | 无限制 | 无限制 | ≤500 | ≤40 | ≤15 | ≤5 | =3 |
| 19∼20 | 无限制 | 无限制 | 无限制 | ≤500 | ≤40 | ≤15 | ≤5 | =0 |
我们按如下方式布局各测试点:
- subtask 1:1∼2,占 10pts。
- subtask 2:3∼4,占 10pts。
- subtask 3:5∼6,占 10pts,依赖 subtask 1,2。
- subtask 4:7∼8,占 10pts,依赖 subtask 2。
- subtask 5:9∼10,占 10pts,依赖 subtask 3,4。
- subtask 6:11∼12,占 10pts,依赖 subtask 4。
- subtask 7:13,占 5pts。
- subtask 8:14∼16,占 15pts。
- subtask 9:17∼18,占 10pts,依赖 subtask 6,7。
- subtask 10:19∼20,占 10pts,依赖 subtask 5,8,9。
各子任务捆绑评测,其分数为该子任务各测试点分数最小值。子任务依赖意味着只有所依赖的子任务分数均非 0 才会评测当前子任务,且分数百分比与所依赖的子任务也取最小值。
接下来阐述关于 o 的特殊性质。
- o=0 时,不保证特殊性质。
- o=1 时,保证输入中 w=0。
- o=2 时,保证输入中 w=2。
- o=3 时,保证输入中 w=0 或 w=1。
- o=4 时,保证输入中 w=0 或 w=2。(该特殊性质没有单独的部分分)
接下来阐述是否输出方案对答案带来的影响。
- 如果选择了 c=0,则答案正确时,你将获得该测试点 80% 的分数,否则该测试点不得分。
- 如果选择了 c=1,则答案和构造方案均正确时,你将获得该测试点的全部分数,否则该测试点不得分。
因此如果你的输出方案可能写错,请慎重考虑是否改为不输出方案。
接下来介绍 checker.cpp 使用方法。
checker.cpp 使用类似于 Testlib 的命令行格式,但是并不基于 Testlib,因此不需要 testlib.h 文件;同时兼容 Lemon 格式。具体的,你可以这么使用:
打开终端,进入 checker.cpp 所在文件夹后,首先使用 g++ checker.cpp -o checker 命令生成可执行文件(需要本地默认采用 C++11 及以上标准)。
假设输入文件为 data.in,输出文件为 data.out,标准答案文件为 data.ans,则你需要将可执行文件 checker 和 data.in/out/ans 文件放置于同一文件夹下,然后在终端中输入如下命令执行:
- 如果你使用 Windows 操作系统,请在 cmd 中使用
checker data.in data.out data.ans执行。 - 如果你使用 Linux 操作系统,请在 bash 中使用
./checker data.in data.out data.ans执行。
稍等片刻即会返回提示信息。
如果你使用 Lemon 来进行本地评测,可以把 checker.cpp 的可执行文件直接作为 Lemon 中的「自定义校验器」使用。
后记
透过指缝观看着那世界末日之景。对立咽了口口水,靠着那股不知名的勇气,将手从自己的脸上移开。
对立伸出了手,把那世界尽头收入了自己所搜集的无数回忆之中。
其余的悲惨记忆,在这枚残片的映衬下显得不足一提。
对立确信自己已经变得足够强大,理所当然地想立刻把一切都摧毁。
就这样,伴随着那抹真诚的微笑与疲惫的笑声,对立从天空中降落到了地面上。
那座古老的塔楼在这般力量驱使下逐渐陨落。
而对立则怀抱着英雄般的信念,坚定不移地迈步向前。