There is a paper strip, whose width is 1, and the widths of every part of it are equal. At the most left position of the strip, there is a vertical line. The strip is soft enough, and it can extend limitlessly to the right side. All points of the paper strip are in one plane.
The strip can fold along a line at a certain position. After the fold, there would be some overlapped parts in the strip, but all points of the paper strip are still in one plane (assuming the thickness of the strip is 0). The horizontal positions of the strip are defined as following: the position of the most left line is 0, and the axis extends to the right alone the strip. The position of a folding line is described by $(a, b)$, "$a$" is the horizontal position of the point of intersection of the line and the strip' top edge, "$b$" is the horizontal position of the point of intersection of the line and the strip'bottom edge. So the folding line is a line through point "$a$" and "$b$".
There are two possibilities for the direction of a fold. Along the folding line, you can fold the left part to the front of the right part or you can fold the left part to the back of the right part. A "fold" $(a, b, d)$ includes the line of folding $(a, b)$ and the direction "$d$" ($0$ for fold the left part to the front, $1$ for fold the left part to the back).
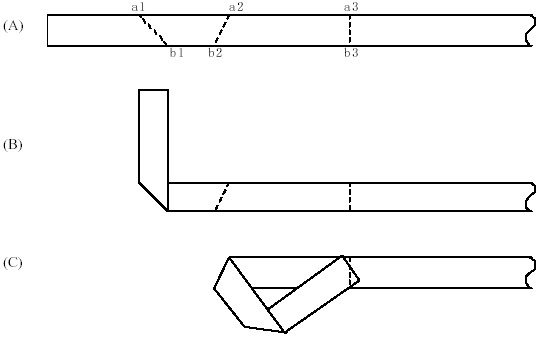
We will list a sequence of folds, $(a_1, b_1, d_1)$, $(a_2, b_2, d_2)$ $\ldots$ $(a_n, b_n, d_n)$, and $a_i \leq a_{i+1}$, $b_i \leq b_{i+1}$ ($1 \leq i < n$), you should fold the strip according to this sequence. If after a fold $i$, the folded part of the strip overlapped the next unfolded folding line $i+1$ at the same side of the paper (that is to say, the direction of fold $i$ and fold $i+1$ are the same), the folding line $i+1$ is called a "failed fold", as is displayed in picture (C).
Write a program to tell if there is failed fold in a sequence of folds.
Input
The input consists of several testcases. The first line of each testcase contains the number of folds in the sequence of folds $n$ ($0 < n \leq 1\,000$). The next line contains $3n$ real numbers, indicating the sequence of folds: $a_1$ $b_1$ $d_1$ $a_2$ $b_2$ $d_2$ $\ldots$ $a_n$ $b_n$ $d_n$.
The end of input is signified by a line consisting of a single $0$.
Output
For each testcase, you should output exactly one single line, consisting of the folding result of the problem. If there is a failed fold in the sequence of folds, output "NO" and followed with the index number of the failed fold. If there is no failed fold, output "YES".
Sample Input
3
3 4 0 6 5.5 0 10 10 0
4
3 3 0 5 5 1 7 7 0 8 8 1
0Sample Output
NO 3
YES