Problem
You are a landlord who owns a building that is an R x C grid of apartments; each apartment is a unit square cell with four walls. You want to rent out N of these apartments to tenants, with exactly one tenant per apartment, and leave the others empty. Unfortunately, all of your potential tenants are noisy, so whenever any two occupied apartments share a wall (and not just a corner), this will add one point of unhappiness to the building. For example, a 2x2 building in which every apartment is occupied has four walls that are shared by neighboring tenants, and so the building's unhappiness score is 4.
If you place your N tenants optimally, what is the minimum unhappiness value for your building?
Input
The first line of the input gives the number of test cases, T. T lines follow; each contains three space-separated integers: R, C, and N.
Output
For each test case, output one line containing "Case #x: y", where x is the test case number (starting from 1) and y is the minimum possible unhappiness for the building.
Limits
Memory limit: 1 GB.
1 ≤ T ≤ 1000.
0 ≤ N ≤ R*C.
Small dataset (12 Points)
Time limit: 240 10 seconds.
1 ≤ R*C ≤ 16.
Large dataset (15 Points)
Time limit: 480 20 seconds.
1 ≤ R*C ≤ 10000.
Sample
4 2 3 6 4 1 2 3 3 8 5 2 0
Case #1: 7 Case #2: 0 Case #3: 8 Case #4: 0
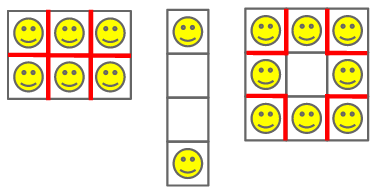
In Case #1, every room is occupied by a tenant and all seven internal walls have tenants on either side.
In Case #2, there are various ways to place the two tenants so that they do not share a wall. One is illustrated below.
In Case #3, the optimal strategy is to place the eight tenants in a ring, leaving the middle apartment unoccupied.
Here are illustrations of sample cases 1-3. Each red wall adds a point of unhappiness.