Problem
Given a vertex-colored tree with N nodes, can it be drawn in a 2D plane with a line of symmetry?
Formally, a tree is line-symmetric if each vertex can be assigned a location in the 2D plane such that:
- All locations are distinct.
- If vertex vi has color C and coordinates (xi, yi), there must also be a vertex vi' of color C located at (-xi, yi) -- Note if xi is 0, vi and vi' are the same vertex.
- For each edge (vi, vj), there must also exist an edge (vi', vj').
- If edges were represented by straight lines between their end vertices, no two edges would share any points except where adjacent edges touch at their endpoints.
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each test case starts with a line containing a single integer N, the number of vertices in the tree.
N lines then follow, each containing a single uppercase letter. The i-th line represents the color of the i-th node.
N-1 lines then follow, each line containing two integers i and j (1 ≤ i < j ≤ N). This denotes that the tree has an edge from the i-th vertex to the j-th vertex. The edges will describe a connected tree.
Output
For each test case, output one line containing "Case #x: y", where x is the case number (starting from 1) and y is "SYMMETRIC" if the tree is line-symmetric by the definition above or "NOT SYMMETRIC" if it isn't.
Limits
Memory limit: 1 GB.
1 ≤ T ≤ 100.
Small dataset (7 Points)
Time limit: 60 10 seconds.
2 ≤ N ≤ 12.
Large dataset (18 Points)
Time limit: 120 20 seconds.
2 ≤ N ≤ 10000.
Sample
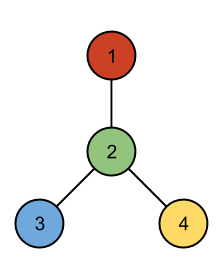
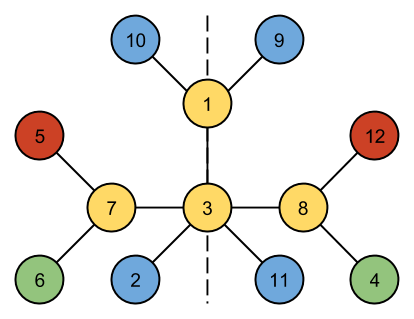
3 4 R G B B 1 2 2 3 2 4 4 R G B Y 1 2 2 3 2 4 12 Y B Y G R G Y Y B B B R 1 3 1 9 1 10 2 3 3 7 3 8 3 11 4 8 5 7 6 7 8 12
Case #1: SYMMETRIC Case #2: NOT SYMMETRIC Case #3: SYMMETRIC
The first case can be drawn as follows:
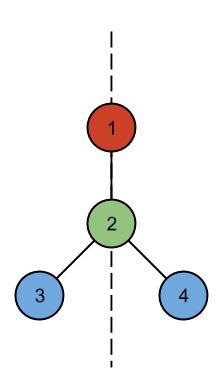
No arrangement of the second case has a line of symmetry: