Problem
Your task in this problem is to find out the minimum number of stones needed to place on an N-by-M rectangular grid (N horizontal line segments and M vertical line segments) to enclose at least K intersection points. An intersection point is enclosed if either of the following conditions is true:
- A stone is placed at the point.
- Starting from the point, we cannot trace a path along grid lines to reach an empty point on the grid border through empty intersection points only.
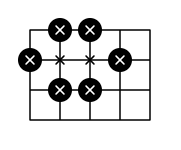
For example, to enclose 8 points on a 4x5 grid, we need at least 6 stones. One of many valid stone layouts is shown below. Enclosed points are marked with an "x".
Input
The first line of the input gives the number of test cases, T. T lines follow. Each test case is a line of three integers: N M K.
Output
For each test case, output one line containing "Case #x: y", where x is the test case number (starting from 1) and y is the minimum number of stones needed.
Limits
Memory limit: 1 GB.
1 ≤ T ≤ 100.
1 ≤ N.
1 ≤ M.
1 ≤ K ≤ N × M.
Small dataset (15 Points)
Time limit: 60 10 seconds.
N × M ≤ 20.
Large dataset (30 Points)
Time limit: 120 20 seconds.
N × M ≤ 1000.
Sample
2 4 5 8 3 5 11
Case #1: 6 Case #2: 8