Problem
You are asked to help diagnose class diagrams to identify instances of diamond inheritance. The following example class diagram illustrates the property of diamond inheritance. There are four classes: A, B, C and D. An arrow pointing from X to Y indicates that class X inherits from class Y.
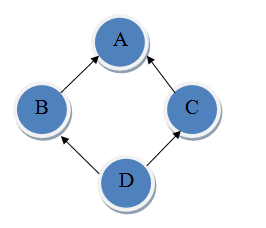
In this class diagram, D inherits from both B and C, B inherits from A, and C also inherits from A. An inheritance path from X to Y is defined as a sequence of classes X, C1, C2, C3, ..., Cn, Y where X inherits from C1, Ci inherits from Ci + 1 for 1 ≤ i ≤ n - 1, and Cn inherits from Y. There are two inheritance paths from D to A in the example above. The first path is D, B, A and the second path is D, C, A.
A class diagram is said to contain a diamond inheritance if there exists a pair of classes X and Y such that there are at least two different inheritance paths from X to Y. The above class diagram is a classic example of diamond inheritance. Your task is to determine whether or not a given class diagram contains a diamond inheritance.
Input
The first line of the input gives the number of test cases, T. T test cases follow, each specifies a class diagram. The first line of each test case gives the number of classes in this diagram, N. The classes are numbered from 1 to N. N lines follow. The ith line starts with a non-negative integer Mi indicating the number of classes that class i inherits from. This is followed by Mi distinct positive integers each from 1 to N representing those classes. You may assume that:
- If there is an inheritance path from X to Y then there is no inheritance path from Y to X.
- A class will never inherit from itself.
Output
For each diagram, output one line containing "Case #x: y", where x is the case number (starting from 1) and y is "Yes" if the class diagram contains a diamond inheritance, "No" otherwise.
Limits
Memory limit: 1GB.
Time limit: 40 8 seconds per test set.
1 ≤ T ≤ 50.
0 ≤ Mi ≤ 10.
Test set 1 (Visible Verdict; 14 Points)
1 ≤ N ≤ 50.
Test set 2 (Hidden Verdict; 14 Points)
1 ≤ N ≤ 1,000.
Sample
3 3 1 2 1 3 0 5 2 2 3 1 4 1 5 1 5 0 3 2 2 3 1 3 0
Case #1: No Case #2: Yes Case #3: Yes