长颈鹿累了,他开始做梦。
在梦中他下坠。他穿过草地,穿过打着转的羊群。他穿过星海,穿过漫天的火羽。
终于,他站在了一块屏幕前。屏幕上展示着某种类似楼梯的图样。
题目描述
我们首先给出一些关于楼梯的形式定义。
我们称一对正整数组成的二元组 $(x,y)$ 为格子,称格子构成的集合 $L$(可以为空)为楼梯当且仅当其满足下面两个条件:
- 若 $(x,y)\in L$ 且 $x>1$,则 $(x-1,y)\in L$。
- 若 $(x,y)\in L$ 且 $y>1$,则 $(x,y-1)\in L$。
对于一个楼梯 $L$ 和 $(x,y)\in L$,我们定义 $(x,y)$ 为生成格生成的子楼梯为
$$\{(a-x+1,b-y+1)\mid(a,b)\in L,a\ge x,b\ge y\}.$$
容易证明这一集合仍然是一个楼梯。对于一个楼梯 $L$,我们定义边界格数为满足 $x=1$ 或 $y=1$ 的 $(x,y)\in L$ 的数量。
为了方便理解,我们接下来给出直观解释。我们在平面上可以将所有格子按从左到右 $y$ 坐标递增、从上到下 $x$ 坐标递增的顺序排列成网格,因此我们也称 $(x,y)$ 为第 $x$ 行第 $y$ 列的格子。
在这一解释下,若一个格子属于某个楼梯,且它上方和左方不是边界,则对应格子也属于这个楼梯。子楼梯就是生成格右下方区域格子所构成的非空楼梯,一个楼梯的边界格数是上边界或左边界上的总格数。
如下图,$(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(4,1),(5,1)$ 组成了一个合法的楼梯。这一楼梯的边界格数为 $8$,其中以 $(1,3)$ 作为生成格生成的子楼梯的边界格数为 $4$。

长颈鹿看到屏幕上的楼梯后很好奇。他首先计算出了这一楼梯的边界格数 $p$,并给定了 $p$ 的某一正整数因子 $q$。他想要知道,给定的楼梯是否有子楼梯满足边界格数等于 $q$。如果是,他希望你给出任一这样的子楼梯的生成格。
梦境时常变化,因此长颈鹿可能会有许多次这样的询问,楼梯也可能会发生变化。初始楼梯 $L$ 为空,对于 $i\ge1$ 记 $s_i$ 为最大的满足 $(i,s_i)\in L$ 的正整数,若不存在则令其为 $0$,则有若干次三种之一的修改:
- 给定正整数 $a$ 和 $b$,在前 $a$ 行的末尾插入 $b$ 格。形式化地,对于 $i=1,2,\cdots,a$,将 $(i,s_i+1),(i,s_i+2),\cdots,(i,s_i+b)$ 加入 $L$。
- 给定正整数 $a$ 和 $b$,在第 $a$ 行后(包含第 $a$ 行)的所有行行末尾删去 $b$ 格,若不足则删空。形式化地,对于 $i=a,a+1,a+2,\cdots,10^{100}$,将 $(i,s_i),(i,s_i−1),\cdots,(i,s_i−b+1)$ 从 $L$ 中移除(不存在的则忽略)。
- 给定正整数 $u$,撤销之前的 $u$ 次操作,即将楼梯还原为 $u$ 次操作前的状态,保证这 $u$ 次操作均为询问或在行末尾插入。具体地,假设该操作为第 $t$ 次操作,我们一定有 $t>u$,且第 $t−1,t−2,\cdots,t−u$ 次操作均为询问或在行末尾插入(即上述的第一种修改)。你只需要将楼梯还原为第 $t−u$ 次操作前的状态即可(当然,你应该保留询问的输出)。
可以证明每次修改之后得到的集合仍然是一个楼梯。
输入格式
输入数据第一行包含一个正整数 $m$,表示操作总数。
接下来 $m$ 行每行描述四种之一的操作,详细含义可参见题目描述一节。描述为由空格分隔的一个字符和一到两个正整数,具体地:
+ a b:在前 $a$ 行的末尾插入 $b$ 格。- a b:在第 $a$ 行后(包括第 $a$ 行)的所有行行末尾删去 $b$ 格,若不足则删空。R u:撤销之前的 $u$ 次操作,即将楼梯还原为 $u$ 次操作前的状态。保证这 $u$ 次操作存在且均为询问或在行末尾插入,即该行之前的 $u$ 行均以+或?开头。? q:询问是否有边界格数等于 $q$ 的子楼梯,若有则给出任意合法生成格。保证 $q$ 是当前楼梯边界格数的因子。
输出格式
对于每个询问(? 操作)输出一行。
如果存在边界格数等于 $q$ 的子楼梯,输出一行两个用空格分隔的正整数 x y,表示一个合法生成格是 $(x,y)$。否则输出一行两个用空格分隔的 $-1$。
样例一
input
18 + 5 1 + 2 1 ? 3 + 3 2 ? 4 ? 4 + 4 1 ? 3 R 3 - 2 2 ? 3 - 1 1 ? 2 ? 4 - 1 2 ? 1 - 9 9 ? 1
output
3 1 1 3 2 2 2 4 2 1 1 2 1 1 1 1 1 1
explanation
每次修改操作之后的楼梯如下图(排列方式同题目描述,省略了各格子的编号)。注意撤销操作实际只撤销了一个 + 操作。样例有多个合法解,给出的输出只是一种合法的输出。
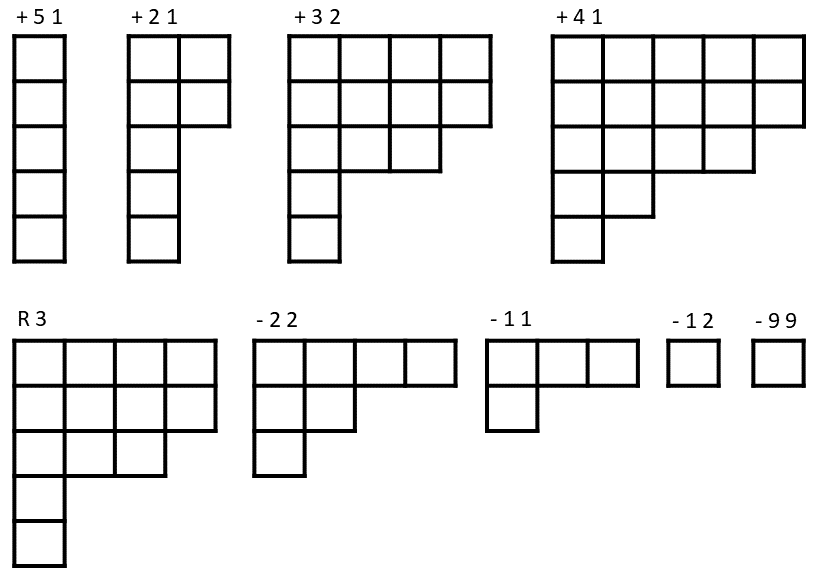
样例二
见下发文件。
样例三
见下发文件。
样例四
见下发文件。
样例五
见下发文件。
样例六
见下发文件。
子任务
对于所有测试数据,$1\le m\le3\times10^5$。
- 对于
+和-操作,$1\le a,b\le10^9$。 - 对于
R操作,保证之前紧邻的 $u$ 次操作存在且均为询问或在行末尾插入。 - 对于
?操作,$1\le q\le10^{18}$ 且保证为当前楼梯边界格数的因子。
记 $a_{\max}$ 为所有 + 和 - 操作中 $a$ 的最大值,$b_{\max}$ 为所有 + 和 - 操作中 $b$ 的最大值。
子任务1(10分):$m,a_{\max}\le 1000$。
子任务2(20分):$m\le 1000$。
子任务3(10分):$m\le 10000$。
子任务4(20分):$m\le 40000$。
子任务5(10分):$m\le 120000$。
子任务6(10分):保证 ? 操作在所有 + 和 - 操作之后。没有 R 操作。
子任务7(20分):无特殊限制。
提示
请注意选用合适的数据类型存储各结果。