Courtney has an avant-garde kitchen counter made out of $N$ rectangular sheets of metal of equal height, standing perpendicular to the ground. When viewed directly from the top, the counter looks like an (unfilled) polygon on a plane with $N$ edges, the $i$th of which extends from point $(X_i, Y_i)$ to point $(X_{(i + 1) \text{ mod } N}, Y_{(i + 1) \text{ mod } N})$. These line segments only intersect at their endpoints.
Courtney's friends often make fun of the counter, saying that the thin metal "surface" is useless for holding anything up, but Courtney wants to prove them wrong.
Courtney considers placing a cup with a circular rim of radius $R$ onto the counter (with the rim facing down), centered at a point chosen uniformly randomly from the square $[0, L] \times [0, L]$. What is the chance that the cup stays balanced on the counter without falling? Your output will be accepted if it is within $10^{-6}$ of the jury's answer.
Note: The face-down cup is modeled as an unfilled ring—not as a disk.
Constraints
- $1 \le T \le 7$
- $1 \le N \le 7$
- $1 \le R, L \le 15$
- $0 \le X_i, Y_i \le 15$
Input Format
Input begins with a single integer $T$, the number of test cases. For each test case, there is first a line containing three space-separated integers $N$, $R$, and $L$. Then, $N$ lines follow, the $i$th of which contains two space-separated integers $X_i$ and $Y_i$.
Output Format
For the $i$th test case, print a line containing "Case #i: " followed by a single real number between $0$ and $1$, the chance that the cup will balance if placed with its rim centered at a uniformly random point in the square $[0, L] \times [0, L]$.
Sample Explanation
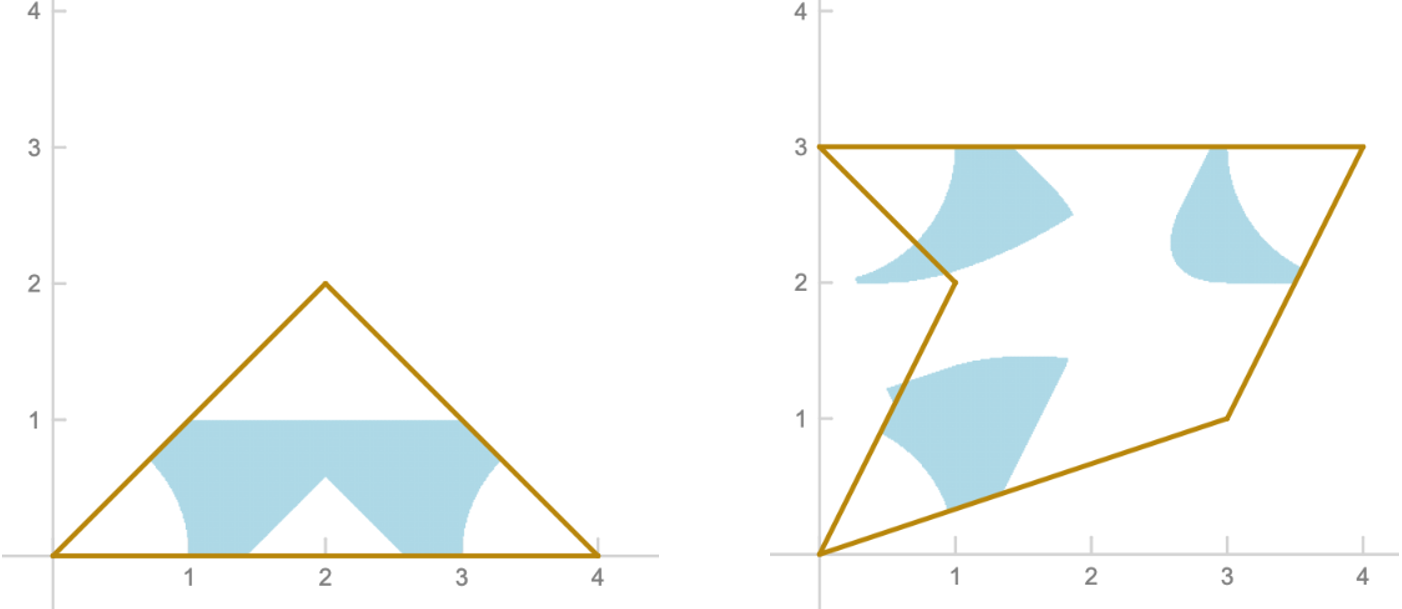
The counters in the first and second sample cases are depicted below, with the blue regions representing points at which centering the cup will lead to it staying balanced.
Sample Input
2 3 1 4 0 0 2 2 4 0 5 1 4 0 0 1 2 0 3 4 3 3 1
Sample Output
Case #1: 0.1169663730642699 Case #2: 0.1353445414060363