Alphabet Adventuring - Problem

Alphonse is assembling an alphabet tree and arranging some adventures along the way.

An alphabet tree is an unrooted tree with $N$ N nodes (numbered from $1$ to $N$) and $N-1$ edges.

Initially, the $i$th edge connects nodes $A_i$ and $B_i$ in both directions, and is labeled with a uppercase letter $C_i$. Two edges incident to a common node are always labeled with different letters.

Alphonse has $Q$ events to process, the $i$th of which is one of two types:

$1$ $U_i$ $L_i$ : Add a new node to the tree by connecting it to node $U_i$ with a new edge labeled with uppercase letter $L_i$. Newly added nodes are numbered with integers starting from $N + 1$ in the order they're added.
$2$ $U_i$ $K_i$ $S_i$ : Print the final node Alphonse will end up at if he:
- Starts a journey at node $U_i$.
- Repeatedly traverses a previously untraversed edge (on this journey). If his current node has multiple untraversed edges, he picks the edge labeled with the letter that comes earliest in the string $S_i$.Ends the journey once there are no more untraversed edges at the current node, or $K_i$ edges have been traversed on the journey.

Please help Alphonse determine where each journey will take him.

Constraints

$1\le T \le 20$
$2\le N \le 300,000$
$1\le Q \le 300,000$
$1\le A_i, B_i \le N$
$A_i \not = B_i$
$C_i, L_i, S_{i,j} \in \{'A', \cdots , 'Z'\}$
$1\le U_i,K_i \le 600,000$

The sum of $N$ over all test cases is at most $1,100,000$.
The sum of $Q$ over all test cases is at most $1,100,000$.

For each event, it is guaranteed that:

$U_i$ is a valid node in the tree at the time of the event.
$L_i$ is different from all existing labels of edges incident to $U_i$ at the time of the event.
$S_i$'s letters are distinct, and are a superset of all edge labels in the tree at the time of the event.

Input Format

Input begins with a single integer $T$, the number of test cases. For each test case, there is first a line containing a single integer $N$. Then, $N - 1$ lines follow, the $i$th of which contains space-separated integers $A_i$ and $B_i$, followed by a space, followed by $C_i$. Then, there is a line containing the single integer $Q$. Then, $Q$ lines follow, the $i$th of which is either $1$ $U_i$ $L_i$ or $2$ $U_i$ $K_i$ $S_i$.

Output Format

For the $i$th test case, print a single line containing "Case #i: ", followed by space-separated integers, the answers to all type-2 events.

Sample Explanation

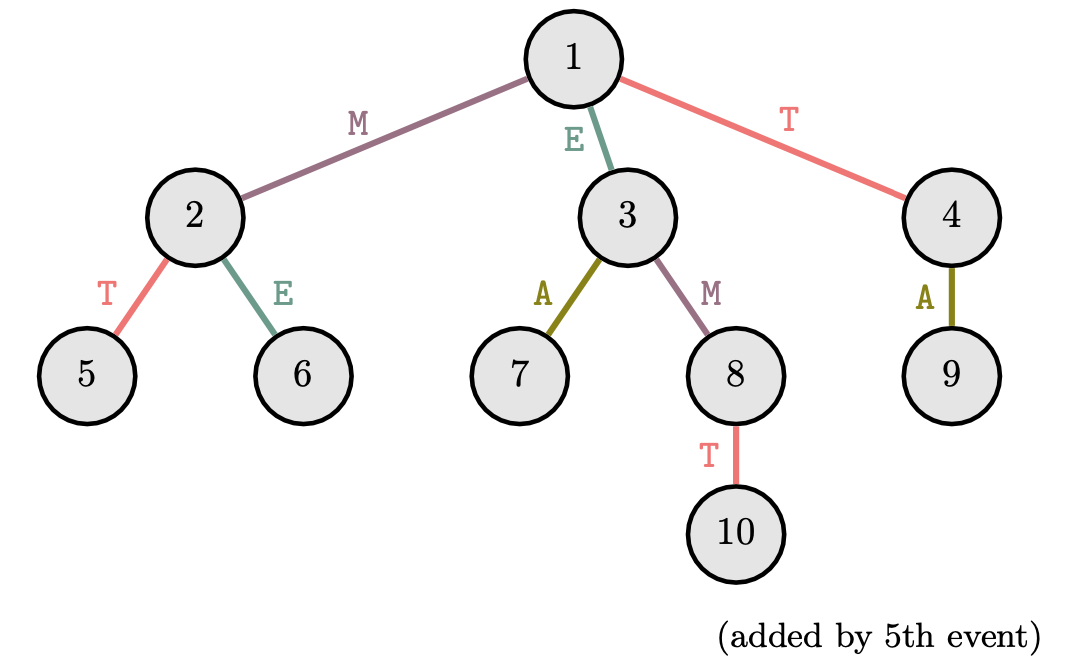
The first sample case's alphabet tree is depicted above, and yields the following journeys:

Event $1$ traverses $1 \stackrel{\texttt{M}}{\longrightarrow} 2 \stackrel{\texttt{E}}{\longrightarrow} 6$ (ended after no more edges from node $6$)
Event $2$ traverses $3 \stackrel{\texttt{E}}{\longrightarrow} 1 \stackrel{\texttt{T}}{\longrightarrow} 4 \stackrel{\texttt{A}}{\longrightarrow} 9$(ended after $K_2=3$ steps)
Event $3$ traverses $9 \stackrel{\texttt{A}}{\longrightarrow} 4 \stackrel{\texttt{T}}{\longrightarrow} 1 \stackrel{\texttt{M}}{\longrightarrow} 2$ (ended after $K_3 =3$ steps)
Event $4$ traverses $8 \stackrel{\texttt{M}}{\longrightarrow} 3 \stackrel{\texttt{E}}{\longrightarrow} 1 \stackrel{\texttt{T}}{\longrightarrow} 4 \stackrel{\texttt{A}}{\longrightarrow} 9$ (ended after no more edges from node $9$)
Event $6$ traverses $8 \stackrel{\texttt{T}}{\longrightarrow} 10$ (ended after no more edges from node $10$)

The second and third sample cases are depicted below.

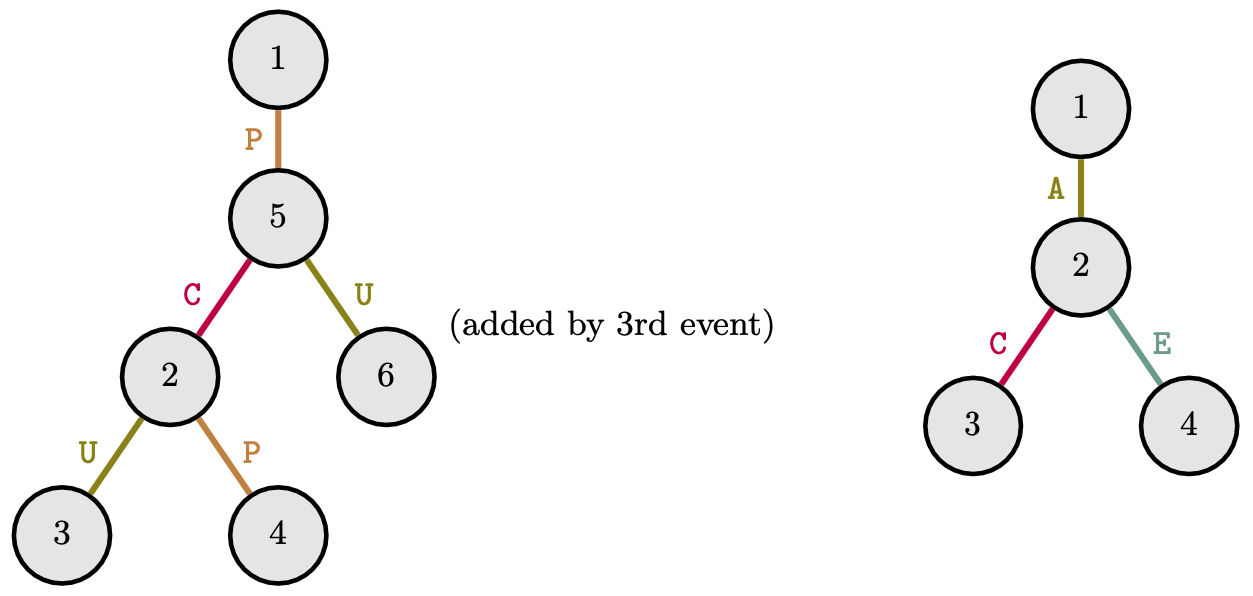
In the second case, the journeys are:

Event $1$ traverses $1 \stackrel{\texttt{P}}{\longrightarrow} 5 \stackrel{\texttt{C}}{\longrightarrow} 2$ (ended after $K_1 = 2$ steps)
Event $2$ traverses $4 \stackrel{\texttt{P}}{\longrightarrow} 2 \stackrel{\texttt{C}}{\longrightarrow} 5 \stackrel{\texttt{P}}{\longrightarrow} 1$ (ended after $K_2 = 3$ steps)
Event $4$ traverses $4 \stackrel{\texttt{P}}{\longrightarrow} 2 \stackrel{\texttt{C}}{\longrightarrow} 5 \stackrel{\texttt{U}}{\longrightarrow} 6(ended after $K_4 = 3$ steps)
Event $5$ traverses $3 \stackrel{\texttt{U}}{\longrightarrow} 2 \stackrel{\texttt{P}}{\longrightarrow} 4$ (ended after no more edges from node $4$)

In the third case, the journeys are:

Event $1$ traverses $3 \stackrel{\texttt{C}}{\longrightarrow} 2 \stackrel{\texttt{A}}{\longrightarrow} 1$ (ended after $K_1 = 2$ steps)
Event $2$ traverses $4 \stackrel{\texttt{E}}{\longrightarrow} 2 \stackrel{\texttt{A}}{\longrightarrow} 1$ (ended after $K_2 = 2$ steps)
Event $3$ traverses $1 \stackrel{\texttt{A}}{\longrightarrow} 2$ (ended after $K_3 = 1$ steps)

Sample Input

3
9
1 2 M
1 3 E
1 4 T
4 9 A
2 5 T
2 6 E
3 7 A
3 8 M
6
2 1 3 META
2 3 3 TEAM
2 9 3 MATE
2 8 8 TEAM
1 8 T
2 8 8 TEAM
5
1 5 P
5 2 C
2 3 U
4 2 P
5
2 1 2 CPU
2 4 3 CUP
1 5 U
2 4 3 CUP
2 3 4 PUCK
4
2 1 A
2 3 C
4 2 E
3
2 3 2 HACKER
2 4 2 REACH
2 1 1 OCEAN

Sample Output

Case #1: 6 9 2 9 10
Case #2: 2 1 6 4
Case #3: 1 1 2

QOJ.ac