题目背景
_往寻奥之星辰_ ----镜(于建安七年(A.D. 0202))
“某年月日,有挚友二人,曰镜曰奥,求索星辰之秘。初苦无所用,次苦无所得。后逢乱,奥迁于外,亦不知所踪矣。区区之身亦可望天命耶,固其情可叹矣。余撰此文以叙之。” ————《荧惑记<序>》
宇宙纪元 1024 太阳年第 256 地球日,于斯特罗法斯星系,“赫希萨基”小行星矿区,“吉伽克”号高级采矿船。
库洛船长本来在阅读几千年前所书写的《荧惑记》,这被考证是人类第一次对于星空的正式的有其科学目的观察记录,可是系统里一阵急促的报警声打扰了他。
“副牵引仓隔离罩人为损坏”船员在系统损管备注里写道,“我们可爱的公主柯娜达又拉来了一块巨大的石头把隔离罩磕坏了,还说要送给马卡那小子”
柯娜达是船长的女儿,马卡是大副的公子,大概还算得上是青梅竹马吧。
库洛船长又开始头痛了,这已经是第三次了,维修科上次就警告过没有多余的当前型号的隔离罩了。
“您还是不要责怪可爱的柯娜达了,”维修科的队长表示,“不过倒可以尝试用那些不能旋转的做一个替代出来,可我算不清楚要开多大的孔。”
作为主脑数据组的一员,库洛船长请你帮助维修科计算一下至少要开多大的孔。
题目描述
隔离罩是用来尽量防止其他宇宙射线对于扫描仪(不是牵引器!)的损坏的重要部件。
简单的,我们可以把切割前的隔离罩看成一个单位球面如下图所示:
工作计划上要完成 $N$($1\leq N \leq 10^6$) 次观测任务。
对于第 $i$ 观测次,我们从点 $(0,0)$ 出发,扫描位于点 $(x_i,y_i,z_i)$,半径为 $r_i$($-10^6 < x_i,y_i < 10^6, 0 < r_i < z_i < 10^6$) 的陨石。 这里我们可以简单的将陨石认为成一个圆球体。
每次观测我们都要保证我们可以通过防护罩上开的洞扫描陨石的全貌。
现在请你计算我们将要开的防护罩上的圆洞在球面上的半径(大圆弧长),即所有陨石球在上半单位球投影的并的最小覆盖圆(这里的圆是在曲面上的)。
由于是单位球,所以这个数值应该等于该圆洞直径上两点与球心连线所呈平面角角度的一半。
显然的,这个角度小于 $\frac{\pi}{2}$ 大于 $0$。若角度为 $\omega \,\mathrm{rad}$ 请你输出 $\frac{\omega}{\pi/2} \times 10^5$ 并向下取整。
输入格式
第一行一个整数 $N$,代表后面有 $N$ 个观测计划。
之后每行四个整数,以空格分割,依序分别为 $x_i,y_i,z_i,r_i$。
输出格式
输出一个范围在 $[0,99999]$ 的整数。
样例数据
样例 1 输入
5
30 10 10 9
100 -10 100 50
-30 100 50 30
12 42 64 20
287 123 46 31样例 1 输出
67877样例 1 解释
下图是各个小行星投影至防护罩的圆和最后挖出来圆洞的示意图。
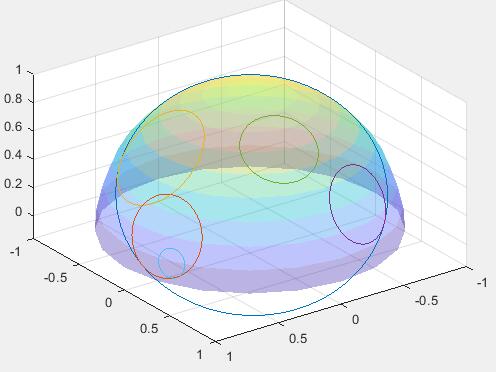
提示
- 这并不是一道计算机图形学题目。
- 背景故事中所有人物、时间、事件、文字均为虚构。
- 输入较大,建议使用更好的读入输出方式。
- 请尽可能地利用您的代数知识。