题目背景

出题人分为 $9$ 种阵营：守序善良、守序中立、守序邪恶、中立善良、绝对中立、中立邪恶、混乱善良、混乱中立和混乱邪恶。真正的出题人，就要能够在阵营之间不断切换，而又不迷失在境界之中。

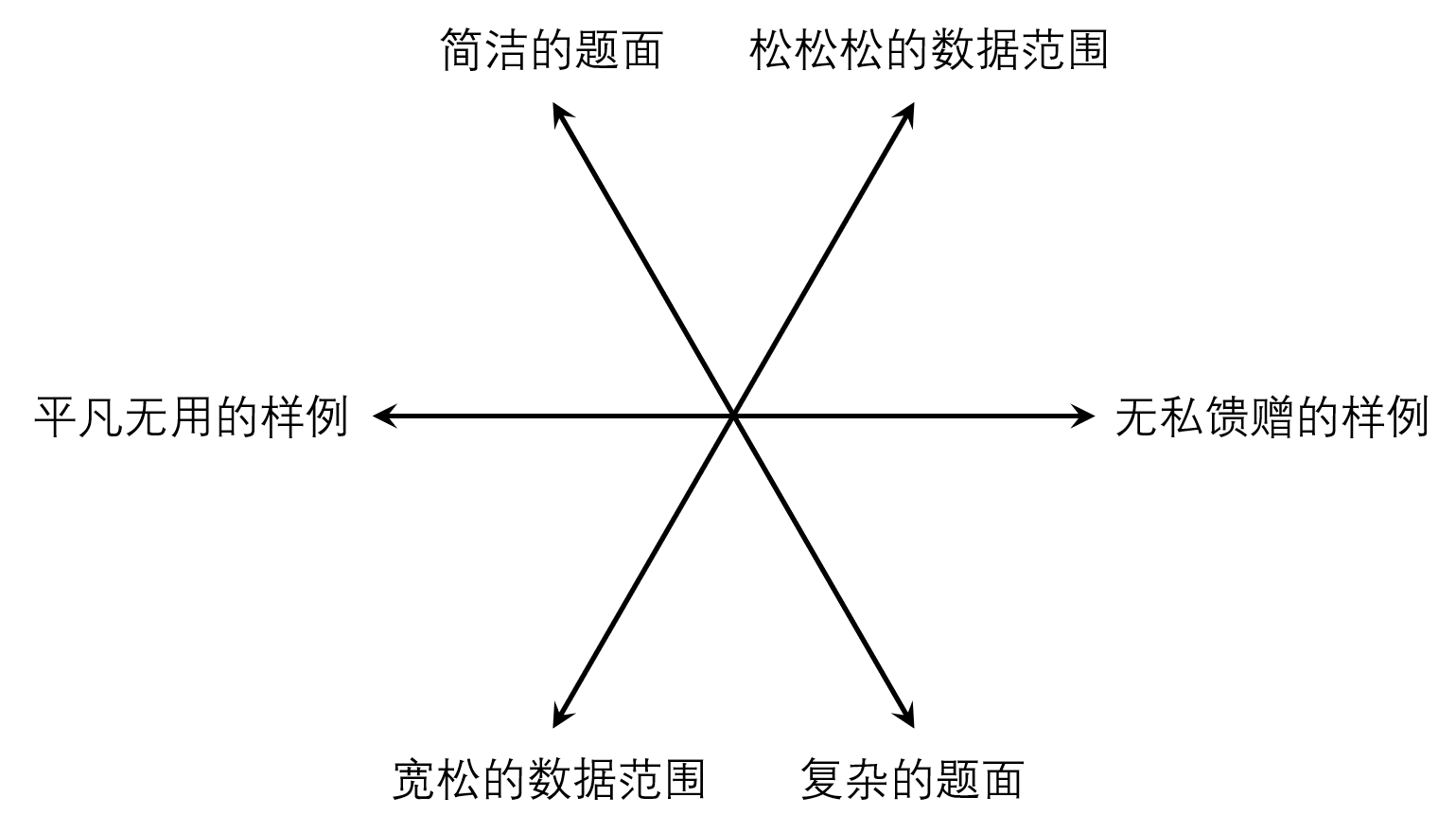
境界是一个无限大的三角形网格。网格如下图，每个交叉点都有 $6$ 个相邻的交叉点。你从某一个交叉点出发，每次给一个出题 idea 设定风格都会使你在境界中移动一步。

题目描述

每个出题人都有一个守序指数 $L$ 和善良指数 $G$。对于一个 idea，从题面、样例或数据范围的角度，可以从 $6$ 个方向中选择恰好一个作为这个 idea 对应的题目的特有风格，同时会在境界中沿着所选的箭头方向移动一步：

你现在一共有 $n$ 个 idea，你知道你给每个 idea 设定某一个风格时你的 $L$ 指数和 $G$ 指数的变化。具体地，对于第 $i$ 个 idea 有 $12$ 个参数 $tl_{i,l},tl_{i,g},l_{i,l},l_{i,g},bl_{i,l},bl_{i,g},br_{i,l},br_{i,g},r_{i,l},r_{i,g},tr_{i,l},tr_{i,g}$：

如果选择“简洁的题面”，那么 $L$ 变成 $L+tl_{i,l}$，$G$ 变成 $G+tl_{i,g}$；

如果选择“平凡无用的样例”，那么 $L$ 变成 $L+l_{i,l}$，$G$ 变成 $G+l_{i,g}$；

如果选择“宽松的数据范围”，那么 $L$ 变成 $L+bl_{i,l}$，$G$ 变成 $G+bl_{i,g}$；

如果选择“复杂的题面”，那么 $L$ 变成 $L+br_{i,l}$，$G$ 变成 $G+br_{i,g}$；

如果选择“无私馈赠的样例”，那么 $L$ 变成 $L+r_{i,l}$，$G$ 变成 $G+r_{i,g}$；

如果选择“松松松的数据范围”，那么 $L$ 变成 $L+tr_{i,l}$，$G$ 变成 $G+tr_{i,g}$。

这里所有的加法都在模 $p$ 意义下进行。

进入混乱邪恶阵营的要求很苛刻，需要 $L$ 恰好等于 $L^*$ 且 $G$ 恰好等于 $G^*$。

你的 $L$ 指数和 $G$ 指数开始时都为 $0$。请问是否存在一种设定风格的方式使得设定完全部 $n$ 个 idea 的风格后你仍在境界中原来的位置，但是能够进入混乱邪恶阵营。

输入格式

第一行两个正整数 $n,p$。

接下来 $n$ 行，每行 $12$ 个非负整数 $tl_{i,l},tl_{i,g},l_{i,l},l_{i,g},bl_{i,l},bl_{i,g},br_{i,l},br_{i,g},r_{i,l},r_{i,g},tr_{i,l},tr_{i,g}$。参数的顺序与题目描述中的一致，无需额外检查。

最后一行两个非负整数 $L^*,G^*$。

输出格式

如果能，输出一行 Chaotic Evil。

如果不能，输出一行 Not a true problem setter。

样例数据

样例 1 输入

3 10
3 5 1 4 9 3 0 0 0 0 0 0
0 0 0 0 0 0 3 5 1 4 9 3
3 5 1 4 9 3 3 5 1 4 9 3
3 2

样例 1 输出

Chaotic Evil

样例 1 解释

给第 $1$ 个 idea 设定风格为”简洁的题面“，此时你的守序指数为 $0+3=3$，善良指数为 $0+5=5$。你往左上方移动一步。

给第 $3$ 个 idea 设定风格为”宽松的数据范围“，此时你的守序指数为 $3+9=2$，善良指数为 $5+3=8$。你往左下方移动一步。

给第 $2$ 个 idea 设定风格为”无私馈赠的样例“，此时你的守序指数为 $2+1=3$，善良指数为 $8+4=2$。你往右边移动一步。此时你回到了原点并且守序指数为 $3$，善良指数为 $2$。所以你可以进入混乱邪恶阵营。

子任务

保证 $n\le 100,p\le 100$。

保证其他输入数据在 $0$ 到 $p-1$ 之间。