题目描述
管道中塞着 $n$ 个彩色的球。这些球的直径相同。从一端到另一端它们的颜色分别为 $c_1,c_2,\cdots,c_n$。
小E有一个空的杯子。杯口的直径恰好比球的直径大一些,所以小 E 可以把球放入杯子中,但一次只能放入一个,并且球在杯子中只能竖直叠放。杯子中两个相邻的同色球会一起消失。
由于管道的特殊性,小 E 每次只能选择管道的一端,将最靠外的球取出,然后马上放进杯子里。
问当管道中的球全部取出后,杯子里最少会剩下几个球,以及在此前提下至少需要多大的杯子。
输入格式
第一行一个正整数 $n$。
第二行 $n$ 个正整数,第 $i$ 个表示 $c_i$。
输出格式
输出一行,包含两个非负整数。第一个数表示杯子里剩下球数的最小值。第二个数表示在此前提下杯子需要至少能装下多少个球。
样例数据
样例 1 输入
12
3 5 1 4 9 3 3 5 1 4 9 3样例 1 输出
0 5样例 1 解释
一种最优的方案如下:
先将两端的 $3$ 放入杯子中消去。
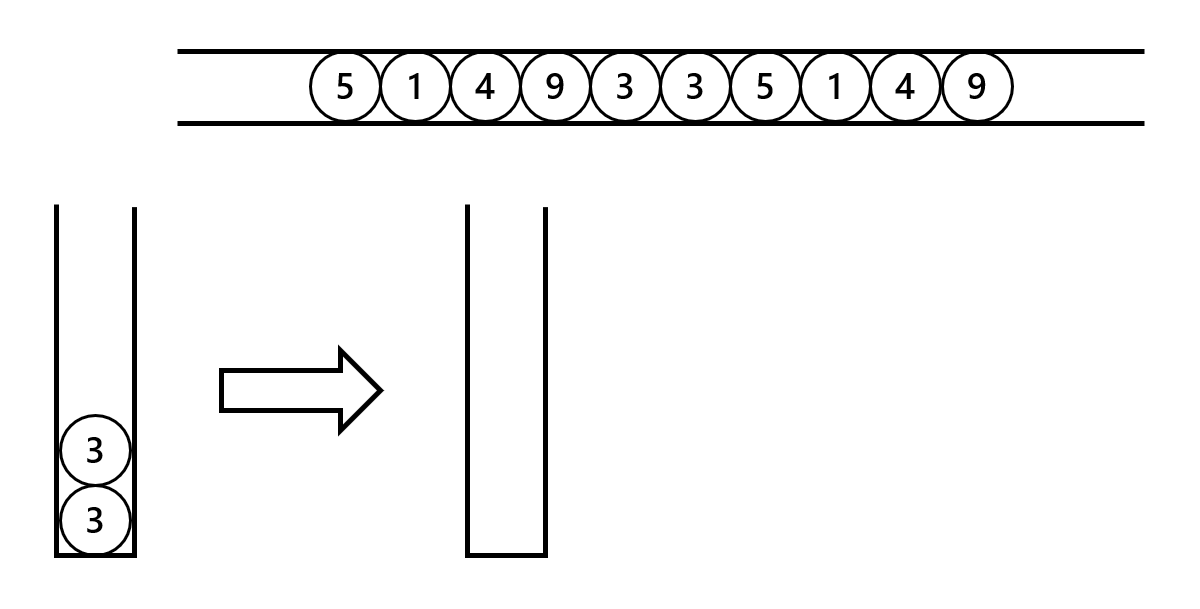
然后把左端的 $5,1,4,9$ 依次放入杯子,这时杯子中有 $4$ 个球。
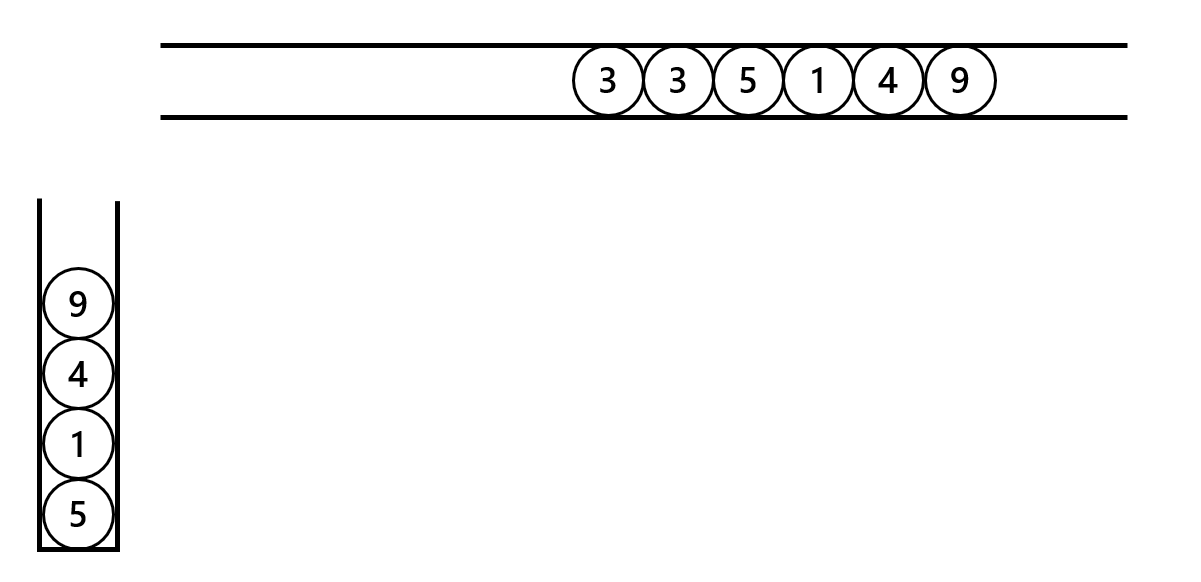
再把右端的 $9,4$ 依次放入杯子,每放入一个球就会和杯子里的另一个球消去。在放入 $9$ 后消去前杯子中有 $5,1,4,9,9$,所以杯子需要能够容纳 $5$ 个球。
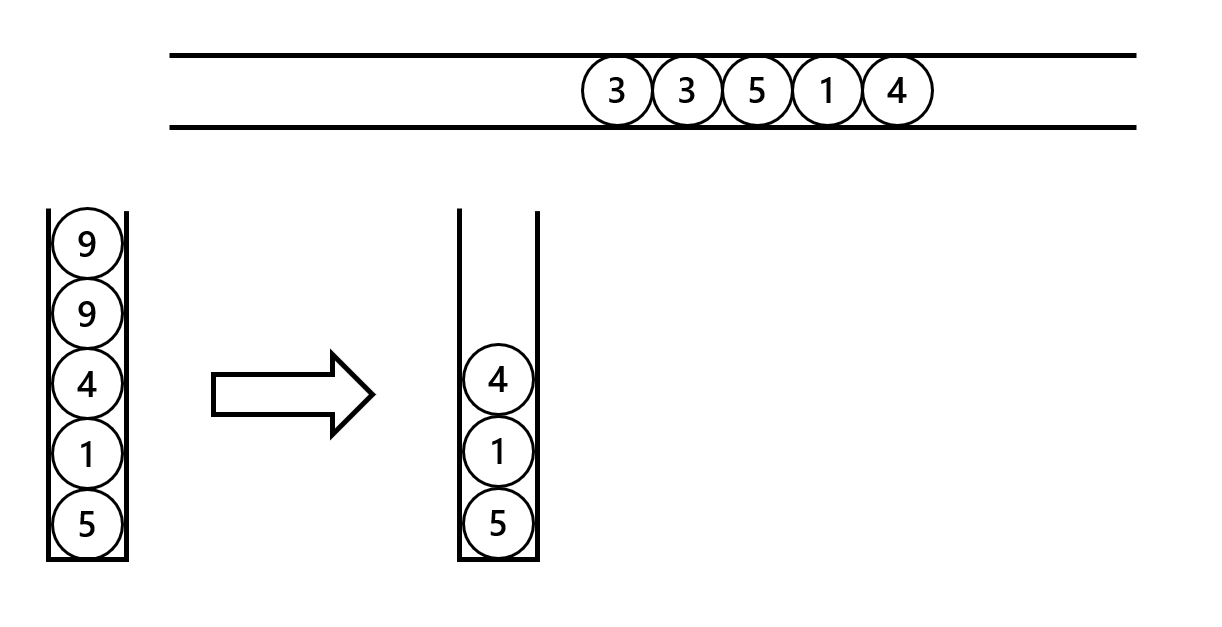
接着把左端的 $3,3$ 放入杯子,这时被杯子中有 $2$ 个球。
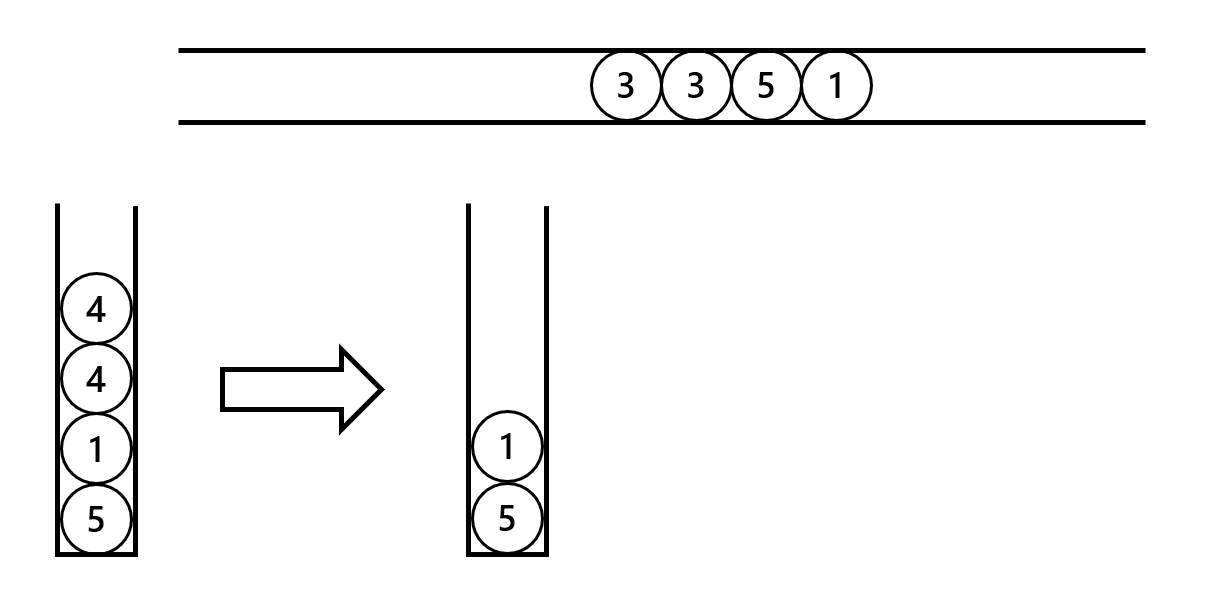
最后把右端的 $1,5$ 依次放入杯子。这时杯子是空的。
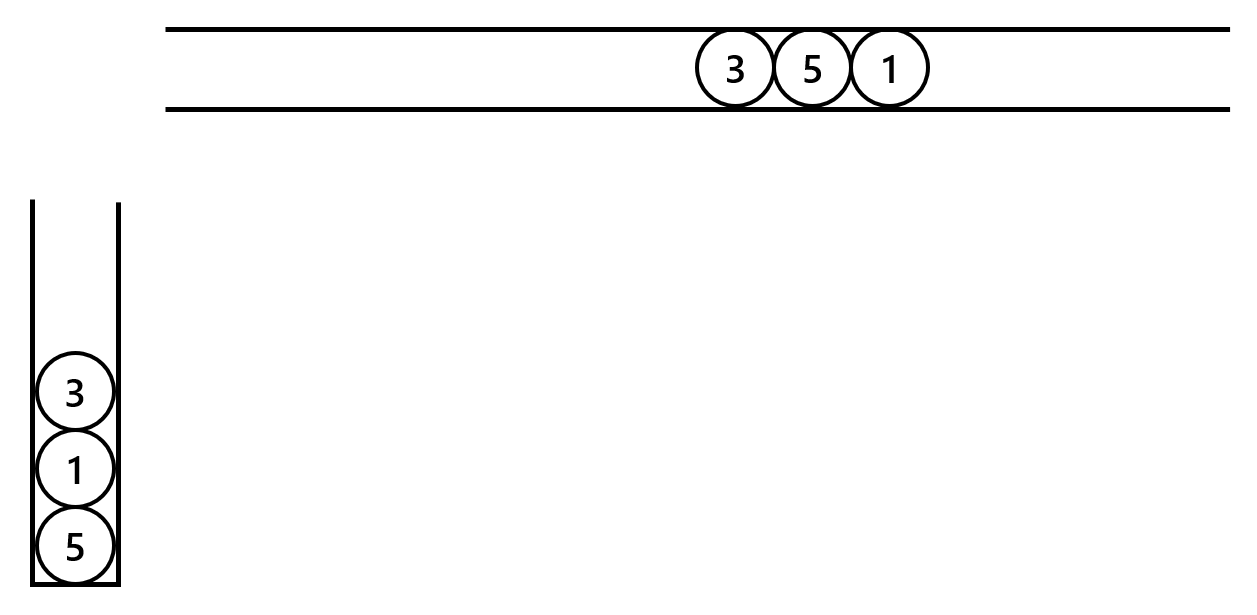
或见下发文件中的 Sampledescription.pptx。
子任务
保证 $n\le 50$,$1\le c_i\le n$。