定向越野是一项集智力与体力为一体的体育运动,在这项活动中,选手需要从起点出发,在尽可能短的时间内到达指定的地点。
牛牛非常喜爱这项运动,但是他不知道怎么样才能更快到达终点。他听说来参加集训的你智力过人,于是他把定向越野的地图交给了你,希望你帮他解决一些问题。
牛牛给你的地图描述的是一块平地,地图上不仅清楚地标出了起点和终点的坐标,还标有若干个互不相交圆形区域,每个区域表示一个圆形的水域。对于不会游泳的牛牛来说,进入水域是根本不可能的。因此,牛牛的行动路线不能从水域中穿过。牛牛想知道这样的路线长度最小可以是多少。
输入格式
第一行包含四个实数 $S_x,S_y,T_x,T_y$ ,分别表示起点的$x,y$坐标和终点的$x,y$坐标。
第二行包含一个整数$n$,表示水域的个数。
接下来$n$行,每行$3$个整数 $x_i,y_i,r_i$ 表示一片水域的圆心的$x,y$坐标和半径。
保证起点和终点都不在水域的内部或边界上,起点和终点不重合。
输出格式
输出一行,包含一个实数,四舍五入精确到小数点后恰好$1$位,表示答案。你的输出必须和标准输出完全一样才算正确。
测试数据保证四舍五入后的答案和准确答案的差的绝对值不大于 $4 \times 10^{-2}$。
(如果你不知道什么是浮点误差,这段话可以理解为:对于大多数的算法,你可以正常地使用浮点数类型而不用对它进行特殊的处理)
样例一
input
2 1 20 11 2 5 5 4 16 9 4
output
23.0
explanation
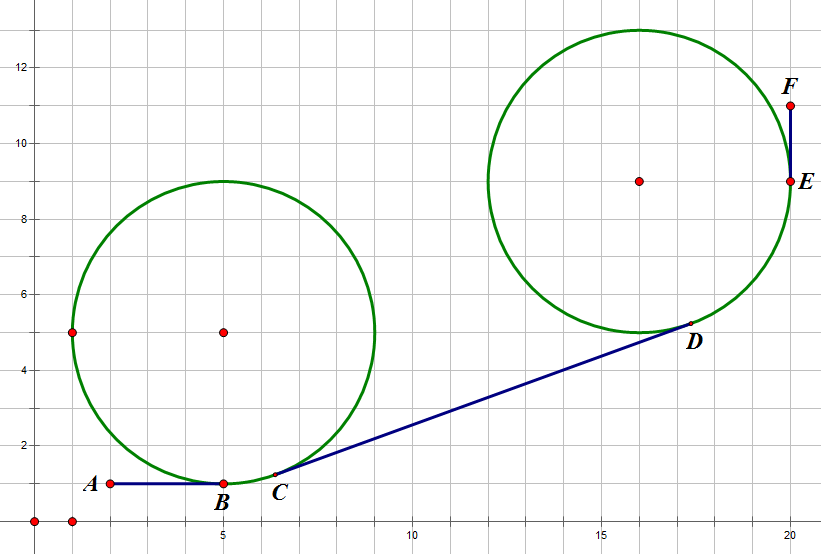
这个地图如下图,其中画出的路径即是所求的最短路径。
样例二
见下发文件。
限制与约定
对于所有数据满足,$0 \le n\le 500, -1000 \le x_i,y_i,r_i,S_x,S_y,T_x,T_y \le 1000$ 。
| 测试点 | $n$ | 半径相同 | 网格 |
|---|---|---|---|
| $1$ | $\leq0$ | × | × |
| $2$ | $\leq1$ | × | × |
| $3$ | $\leq1$ | × | × |
| $4$ | $\leq2$ | √ | × |
| $5$ | $\leq2$ | × | × |
| $6$ | $\leq3$ | × | × |
| $7$ | $\leq4$ | √ | √ |
| $8$ | $\leq5$ | × | × |
| $9$ | $\leq8$ | × | × |
| $10$ | $\leq16$ | √ | √ |
| $11$ | $\leq20$ | × | × |
| $12$ | $\leq50$ | √ | × |
| $13$ | $\leq100$ | √ | √ |
| $14$ | $\leq200$ | × | × |
| $15$ | $\leq400$ | √ | √ |
| $16$ | $\leq400$ | √ | √ |
| $17$ | $\leq500$ | × | × |
| $18$ | $\leq500$ | × | × |
| $19$ | $\leq500$ | × | × |
| $20$ | $\leq500$ | × | × |