在一个 $N \times M$ 个方格组成的棋盘内,有 $K$ 个方格被称为特殊方格。我们要使用一组俄罗斯方块来覆盖这个棋盘,保证特殊方格不能被覆盖,非特殊方格只能被一个俄罗斯方块覆盖,求最多能容纳的俄罗斯方块的数量。
已知有以下三组俄罗斯方块,一个棋盘可能用其中的某一组。
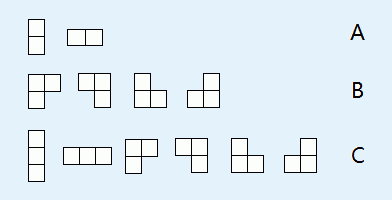
输入格式
第一行三个整数,$N,M,K$,和一个字符,$type$,为所用的俄罗斯方块组。
接下来 $K$ 行每行两个整数,$X,Y$,表示第 $X$ 行第 $Y$ 列为特殊方格。
输出格式
一个整数,为所求的答案。
样例数据
样例 1 输入
8 8 0 A样例 1 输出
32样例 2 输入
7 6 6 C
3 1
3 6
5 3
5 4
5 7
6 7样例 2 输出
12子任务
| 测试点 | $N, M$ | $K$ | $type$ |
|---|---|---|---|
| $1 \sim 6$ | $0 < N,M \leq 100$ | $0 \leq K \leq NM$ | A |
| $7 \sim 12$ | $N=M=2^L,\ 0 < L \leq 200\,000$ | $K=1$ | B |
| $13 \sim 20$ | $0 < N,M \leq 11$ | $0 \leq K \leq NM$ | C |