小Y是一个爱好旅行的OIer。一天,她来到了一个新的城市。由于不熟悉那里的交通系统,她选择了坐地铁。
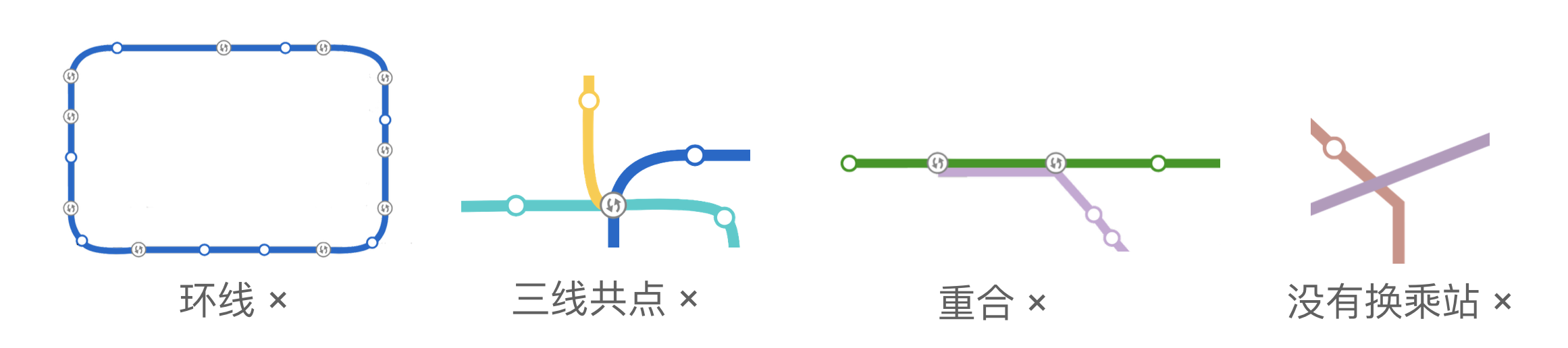
她发现每条地铁线路可以看成平面上的一条曲线,不同线路的交点处一定会设有换乘站  。通过调查得知,没有线路是环线,也没有线路与自身相交。任意两条不同的线路只会在若干个点上相交,没有重合的部分,且没有三线共点的情况。即,如图所示的情况都是不存在的:
。通过调查得知,没有线路是环线,也没有线路与自身相交。任意两条不同的线路只会在若干个点上相交,没有重合的部分,且没有三线共点的情况。即,如图所示的情况都是不存在的:
小Y坐着地铁 $0$ 号线,路上依次经过了 $n$ 个换乘站。她记下了每个换乘站可以换乘的线路编号,发现每条线路与她所乘坐的线路最多只有 $2$ 个换乘站。现在小Y想知道,除掉她经过的换乘站以外,这个城市里最少有几个换乘站。只有你告诉她正确的答案,她才会答应下次带你去玩呢。
输入格式
从标准输入读入数据。
请注意本题有多组输入数据。
输入数据的第一行是一个整数 $T$,表示输入数据的组数。接下来依次给出每组数据。
对于每组数据,第一行是一个整数 $n$,表示小Y经过的换乘站的数目。第二行为 $n$ 个用空格隔开的整数,依次表示每个换乘站的可以换乘的线路编号。这些编号都在 $1$ ~ $n$ 之内。
输出格式
输出到标准输出。
对于每组输入数据,输出一行一个整数,表示除掉这 $n$ 个换乘站之外,最少有几个换乘站。
样例一
input
4
4
1 2 1 2
8
1 2 3 4 1 2 3 4
5
5 4 3 3 5
8
1 2 3 4 1 3 2 4output
0
0
0
1explanation
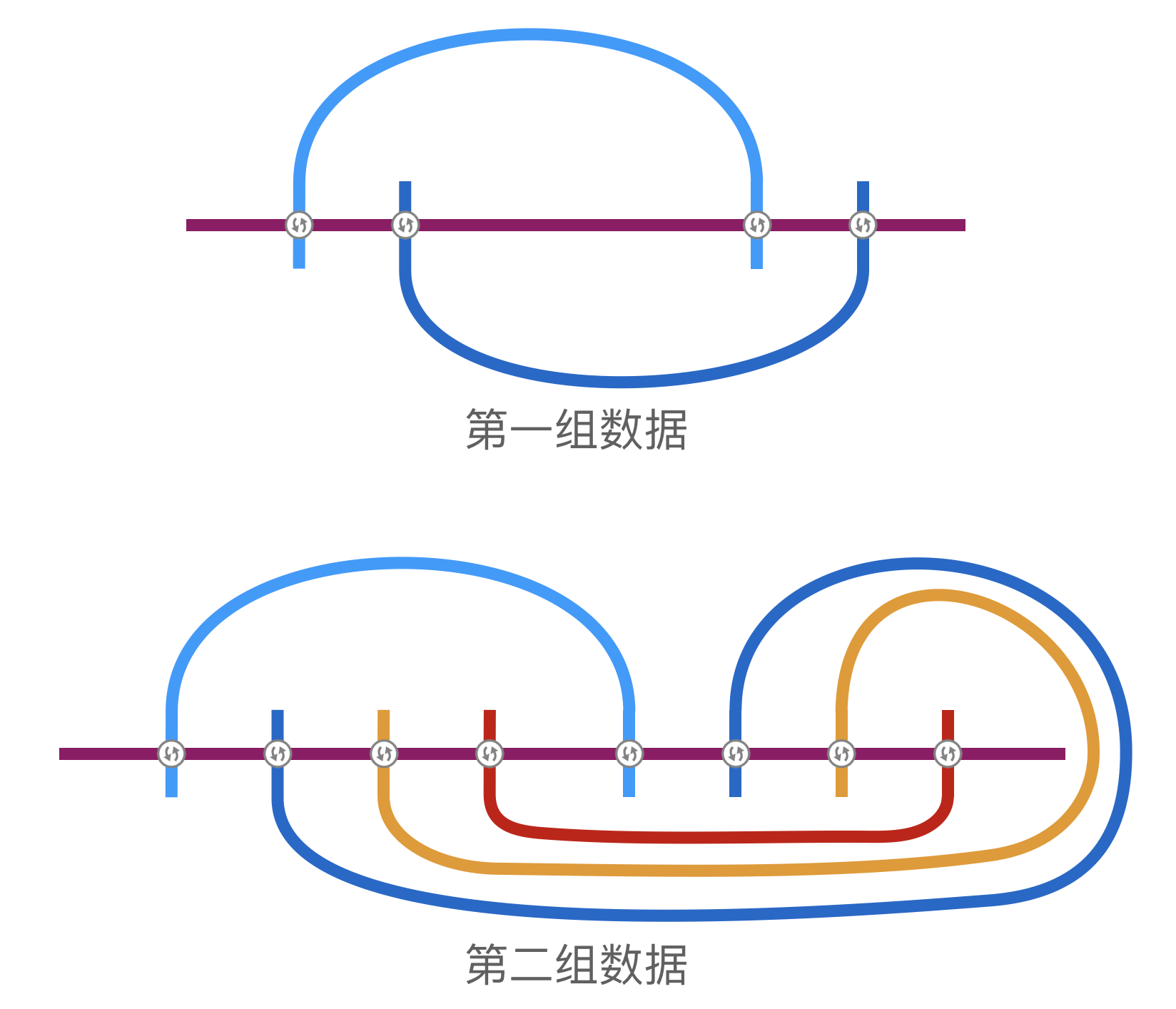
对于样例的前两组数据,一种可能的最优答案如下图所示。
限制与约定
一共有 50 个测试点,每个测试点 2 分。你只有在答案完全正确时才能得到该测试点的全部分数,否则不得分。
对于所有测试点,以及对于样例,$1 \le T \le 100, 1 \le n \le 44$。对于每个测试点,$n$ 的范围如下表:
| 测试点编号 | $1 \le n \le$ | 测试点编号 | $1 \le n \le$ |
|---|---|---|---|
| 1 | 2 | 26 | 32 |
| 2 | 3 | 27 | 33 |
| 3 | 4 | 28 | 33 |
| 4 | 5 | 29 | 34 |
| 5 | 6 | 30 | 34 |
| 6 | 8 | 31 | 35 |
| 7 | 9 | 32 | 35 |
| 8 | 10 | 33 | 36 |
| 9 | 11 | 34 | 36 |
| 10 | 12 | 35 | 37 |
| 11 | 13 | 36 | 37 |
| 12 | 14 | 37 | 38 |
| 13 | 15 | 38 | 38 |
| 14 | 16 | 39 | 39 |
| 15 | 17 | 40 | 39 |
| 16 | 20 | 41 | 40 |
| 17 | 22 | 42 | 40 |
| 18 | 24 | 43 | 41 |
| 19 | 26 | 44 | 41 |
| 20 | 28 | 45 | 42 |
| 21 | 30 | 46 | 42 |
| 22 | 30 | 47 | 43 |
| 23 | 31 | 48 | 43 |
| 24 | 31 | 49 | 44 |
| 25 | 32 | 50 | 44 |