题目描述
给一个边长为 $n$ 的正三角形,其被分成了 $n^2$ 个小的边长为 $1$ 的正三角形,其中有 $\frac{n(n+1)}2$ 个正着的, $\frac{n(n-1)}2$ 个倒着的。现在有 $n$ 个正着的三角形被切掉了,剩下 $\frac{n(n-1)}2$ 个正着的和 $\frac{n(n-1)}2$ 个倒着的。问能否用 $\frac{n(n-1)}2$ 个夹角为 $60^\circ$ 和 $120^\circ$ ,边长为 $1$ 的菱形覆盖所有小三角形。如果有,输出一种方案。
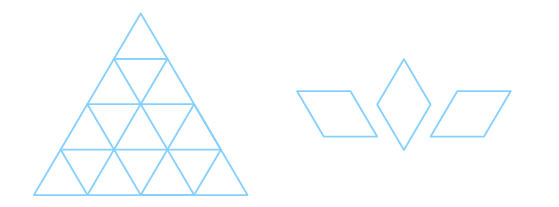
一个边长为 $4$ 的正三角形 三种不同的菱形,从左到右标号为 $1,2,3$
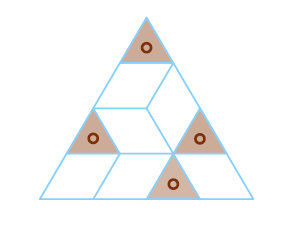
一种 $n=4$ 的例子
输入格式
第一行一个正整数 $n$ ,代表大正三角形的边长。
接下来 $n$ 行,第 $i(2\leq i\leq n+1)$ 行一个长度为 $i-1$ 的 $01$ 字符串,第 $j$ 个字符为 $0$ 代表第 $i$ 行第 $j$ 个正着的小三角形被切掉了。
输出格式
如果没有一种合法的菱形覆盖的方式,输出 Impossible! 。
否则输出任意一组合法解。合法解一共包含 $n$ 行,第 $i$ 行为一个长度为 $i$ 的字符串,第 $i$ 行第 $j$ 个字符表示第 $i$ 行第 $j$ 个正着的小三角形的情况,具体格式如下:
- 如果第 $i$ 行第 $j$ 个字符为 $'-'$,代表这个小三角形被切掉了。
- 如果第 $i$ 行第 $j$ 个字符为 $'1'$,代表这个小三角形被第一种菱形覆盖。
- 如果第 $i$ 行第 $j$ 个字符为 $'2'$,代表这个小三角形被第二种菱形覆盖。
- 如果第 $i$ 行第 $j$ 个字符为 $'3'$,代表这个小三角形被第三种菱形覆盖。
样例输入
4 0 11 010 1101
样例输出
- 21 -3- 33-1
数据范围
保证 $n\leq 5000$ 。
subtask1(5pts) : $n\leq 5$ 。
subtask2(10pts) : $n\leq 10$ 。
subtask3(35pts) : $n\leq 500$ 。
subtask4(5pts) :保证每一行恰好有一个正着的小三角形被切掉。
subtask5(15pts) :保证存在一组解。
subtask6(30pts) :无特殊限制。
时间限制:2s
空间限制:1GB